電磁気では、電流と変化する電界で渦磁界が発生し、変化する磁界は渦電界を作る性質が次々につながり交流では高調波が発生したり、電磁波(電波・マイクロ波・光・放射線・ガンマ線)を作り出す。その理解には微分と積分とベクトルと回転による位相と複素数の考え方が必要です。
マクスウェル方程式の第3式は、「電流」と「電界の変化」が磁界をつくる(右ネジの法則)、
第4式が、コイル中の磁界(磁束)の変化が電界(電圧)をつくる法則の説明。
ローレンツ力は、磁界の中を電気が通る時に働く力(右ネジの法則)で、モーターが働く原理。
(モーターが回る説明方法には、外側の磁界と回転子の磁界が引っ張り合ったり反発しあったりで説明することもある)。
※右手の法則は、右手の親指を電流の方向にすると、他の指を丸めた方向の渦状の磁界が発生。
コイルに電流を流すと巻き線の周りの磁界がつながって、コイルに流れる電流方向が右手の人差し指~小指とすると、コイルの中の磁界は親指方向となる。
※左手の法則は、「人差し指が磁力線の向き,中指が電流の向きを示すようにすると,親指の方向に向いた力が導線に働く」。掛け算のベクトル順番が逆。

ベクトルだと電磁気力の関係式が1行に。
なんて簡潔!使わにゃ損だ。
電流の回りにできる回転磁界(右手の法則)は、ベクトルでは
rotH=I (なんて簡潔!)
真空中では電流がないので(電界と磁界が相互に影響しあって電磁波ができる基本式)
rotH= ∂D/∂t (なんて簡潔!)
rotE= – ∂B/∂t (なんて簡潔!)
※ 偏微分記号 ∂ は 「でる」 で変換できます! 分母∂tはt以外は一定でtだけがわずかに変化するときの分子側の変化量を意味します。
ローレンツ力という電流 i が磁界 B から受ける力は
F=ixB ベクトルの外積(なんて簡潔!)。
力が働く時に、方向と大きさを持つ「力」は、ベクトルであらわせる。
ある方向に長さLだけ、力Fをかけながら動かすと、力が行った仕事は、
W=F・L ベクトルの内積 (なんて簡潔!)。
同じ方向の場合は、力x長さ ですが、直角方向に動く時は 力x長さxcosΘ で 0 になります。
円運動から生まれる電流の説明には円運動の数学が便利
電気では、工業的に使う場合はほとんどが交流です。
交流電気は、発電機の回転から生み出されので、円運動が理解の基礎になります。
円運動とそれにかかわる数学(複素数平面とオイラーの公式)使うと、交流現象を簡潔に表現できる!
複素数を利用すると、交流波形の微分・積分が90度位相が進む・遅れるに変換され、コンデンサーのコンダクタンス・コイルのインピーダンスが、簡単に表現できてしまいます。
円運動は、半径一定で角度が増える運動、その(x、y)座標を示すのが三角関数のsinとcos
マクスウェルの方程式は、磁界の変化(=微分)が変化を妨げる方向の電界を作ると。
なので、sin cos の変化を示す微分の理解が鍵となる。
交流回路で複素数を使う理由とオイラーの公式の使い方
電気屋さんのひとりごと https://eleeleinfo.com/blog-ac-circuit-theory/
は、交流の現象を理解するのに、複素数やオイラーの公式を使うと微分・積分・位相差などが簡単に表現でき
三角関数の微分が位相を90度進め、積分は90度遅らせことがわかります。
(動画で解説)オイラーの公式【応用数学A・複素関数編】(東北大学の授業編)
初めての概念は動画で見るのが早道
趣味人のブログ より . 正弦波の複素数表示
このサイトは簡潔でわかりやすい説明が特徴。
正弦波を時間微分すると正弦波となり,角周波数は変化せず,振幅は ω 倍,かつ位相は π / 2 進む.
正弦波を時間積分すると正弦波となり,角周波数は変化せず,振幅は1 / ω 倍,かつ位相は π / 2 遅れる
下記のサイトは、より詳しく、具体的に電気を扱うときの計算方法を高校・大学の数学を使って統合的にわかりやすく解説。
交流(複素数表示) https://physnotes.jp/em/ac_complex/
この内の一部をご紹介
=====================================
このように, 複素電圧 というものを考え, 現実に観測できる交流電圧と複素電圧とを下図のように対応させる考え方を(電圧の)複素数表示という.

<電流やインピーダンスなど以下省略>
=====================================
交流回路にある3種(抵抗・コンデンサー・コイル)の働き
ネットからわかりやすい解説を引用で紹介します
抵抗のみの回路の交流電流
波形の頂点と0になる時間的なズレが発生しません。
電圧eと電流iは同相になります。
コイルのみの回路の交流電流
コイルのみの交流回路では電圧に対して電流の位相が90°遅れます。
波形の頂点と0になるタイミングが電流が90°遅くなります。
これはコイルに電流の変化を嫌う性質(今の電流を維持したい)があるので、電圧に対して電流が遅れて変化する為です。
コンデンサのみの回路の交流電流
コンデンサのみの交流回路では電圧に対して電流の位相が90°進みます。
波形の頂点と0になるタイミングが電流が90°早くなります。
コンデンサは電圧の変化を嫌う性質があります。(かかっている電圧を維持するためにたくさんの電流を流そうとする)
=======================
交流回路の説明には、「位相」が早くなる・遅くなるという言葉がでてきます。
位相ってなんだ?を理解する必要がありそうだ。
位相は、回転運動するときの角度を意味します。位相が進むとは回転位置が先に進むこと、遅れるとは逆に回転位置が送れること。
どうやったらそれを表現できるのだろうか?
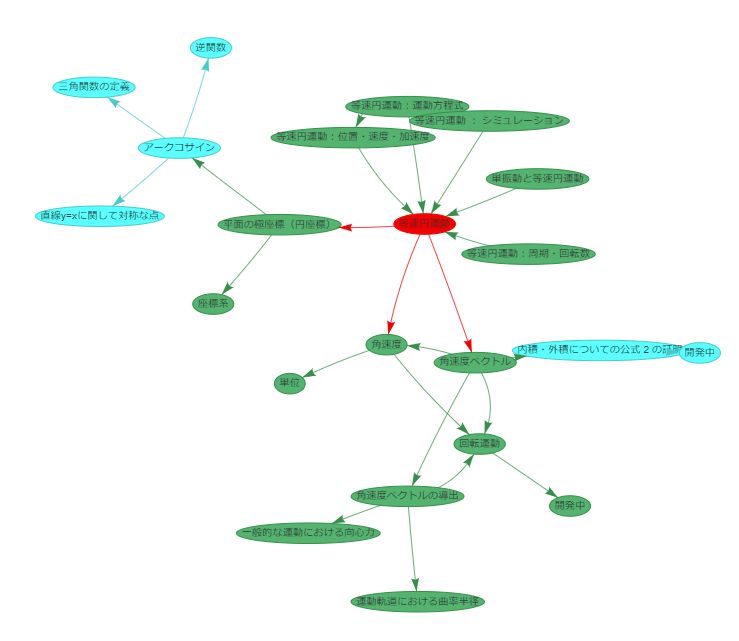
金沢工業大学が、等速円運動に関係する数学概念の関係図を解説
スタートになる概念の等速円運動がこれ。
rを1とすると Pの位置は P(x=sinΘ, y=cosΘ)。
等速円運動 (uniform circular motion)
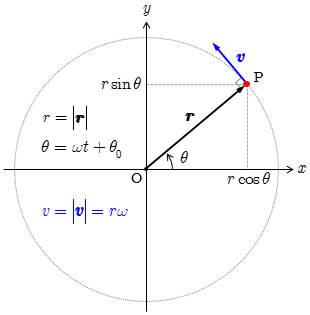
物体が円周上を一定の速さで運動しているとき,その運動を 等速円運動 (uniform circular motion) という.
進学塾 東大塾長の理系ラボ から引用でご紹介
https://rikeilabo.com/trigonometric-function-graph
三角関数のグラフって?この解説が分かりやすい
1. 三角関数のグラフの書き方
まずは基本となる「y=sinθ」「y=cosθ」「y=tanθ」のグラフの書き方からやっていきましょう。
1.1 y=sinθ のグラフ
y=sinθ の値は、次の表のようになります。

したがって、y=sinθ のグラフは次のようになります。

- 周期は 2π
- θ は実数全体,−1≦y≦1
- 原点に関して対称(奇関数)
1.2 y=cosθ のグラフ
y=cosθ の値は次の表のようになります。

したがって、y=cosθ のグラフは次のようになります。

- 周期は 2π
- θ は実数全体,−1≦y≦1
- y 軸に関して対称(偶関数)
また、y=sinθ,y=cosθ のグラフを正弦曲線といいます。