電波は電磁波という波だという。電気の交流もその電位は電線を光速で伝わる波だという！

じゃ、波ってなんなんだろう？

調べると、波は「波動方程式」をみたすものなんだと。
波とは、たった1行の2階偏微分方程式をみたすものだと。じゃ、その方程式とその意味とは？
ある現象が、場所と時間で表現され、場所と時間それぞれの、２階偏微分（変化（偏微分）の変化（さらに偏微分））が同じ形になるものが波だと。
電磁気では、電界の時間微分が磁界になり、その時間微分が電界になる、2回微分すると元になる、ようなものが波。

マクスウェル方程式で真空中では電流がないから、電界の時間偏微分が磁界の位置の偏微分、磁界の時間微分が電界の位置微分、それぞれの微分が同じ値になるということは磁界も電界も相互に直交し同位相ということ。

電界が　sin　なら　微分は　cos　、それが磁界の位置偏微分になるので磁界はその積分になって　sin　！
なので、同位相の互いに垂直な波として電界・磁界の同位相の波に直交する方向に光速で進む波になると。

波の様相を　https://www.ccs-inc.co.jp/guide/column/light_color/vol02.html　から引用でご紹介

≪※1≫ 電磁波

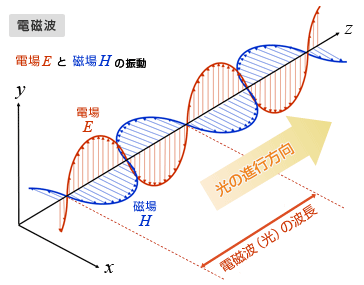
電磁波とは、空間の「電場 （ electric field ） E 」 と「磁場 （ magnetic field ） H 」が互いに振動しながら空間を伝播していく物理現象です。

 

http://fujisawa.phys.titech.ac.jp/fujisawa/PhysCText-Wave10pt.pdf
は、少々長いテキストですが波一般を詳しく紹介しています。そして電磁波についても解説しています。
部分引用でご紹介。

---

この式の形をみると、y(x,t)=f(x-ωt)+g(x+ωt)　になっています。
1項目は右に速度ωで進む（平行移動）任意の関数、2項目は左に速度ωで進む（平行移動）任意の関数で、その重ね合わせ。

※y=f(x)　に対して　y=f(x-ωt)　は形が同じで、右方向にωの速度で進む（原点が平行移動）こと。
　波らしい関数としてsinを取ると、
　y(x,t)=sin(x-ωt)は、時刻ｔを固定すればx軸上で原点が右側にωtだけ移動したsinの曲線。
　時刻tが増える分だけｘ軸上で右に進むsin曲線を意味します。

そして sinの微分は　cos　で　その微分は　-sin　で、xでもtでも2回偏微分すると係数の2乗を除き同じ形になります。
（符号は　++で＋、　- -で+）　偏微分とは、微分する変数以外は定数とみなします。

このように、左右が同じになります。波が進む形の（ｘ－ｃｔ）がポイントなんですね。
空間と時間が速度を介してセットになる関係が波の本質のようです。

これを難しい偏微分方程式の数式による解ではなく、直感的にわかりやすく動画で解説しているものがありました。
わずか11分です。数学は難しい証明問題は数学者に任せ、その意味するところをイメージし利用することが大事。

実はめちゃくちゃ直感的。波動方程式の本当の意味。

 

 

電磁波に関する数学・物理学的により詳しい説明では、次に紹介する東京工業大学のテキストが簡潔です

第 13 講 Maxwell の方程式と電磁波

http://www.th.phys.titech.ac.jp/~muto/lectures/Gelmg06/Gem_chap13.pdf

真空中では、電流がなく磁界の湧き出しもないことから、マクスウェル方程式にｘ方向にだけ進む波として、関数はｘと時間ｔだけと仮定し、マクスウェル方程式を解くと、波動方程式が得られると。
前提　電流なしdiv Ex =0  、 磁界の湧き出しなしdiv Bx = 0、  rot（渦）は回転軸成分の偏微分が0（回転するコマには軸方向には変化がないため）

ポイント部分を引用でご紹介。

前の講までに学んだ電場と磁場の法則を組み合わせて整理すると，電磁気学の基本的な４つの方程式，すなわち，Maxwell の方程式が得られる。ただし，その際，変位電流の概念を導入して Amp`ere の法則を一般化する。また，Maxwell の方程式から波動方程式が導かれ，その解として電磁波が存在する。

＜まとめ＞
　Ez と By は同じ関数 f と g で表され，両者が互いに組み合って，離れることなく，同じ速さ v をもつ波動となって x 軸にそって伝播する。これを 電磁波（electromagnetic wave）と呼ぶ。
　電磁波は，振動する電場（Ez）と磁場（By）の方向が，いずれも波の進行方向（x 軸方向）に垂直になっており，横波である。進行方向に振動する縦波成分（Ex，Bx）は存在しない。
　また，電場の振動方向（z 軸方向）と磁場の振動方向（y 軸方向）は垂直である。
　さらに，x 軸の正の向きに進行する電磁波において，電場が z 軸の正の向きであるとき（Ez > 0），磁場は y 軸の負の向きである（By < 0）。すなわち，電場，磁場，及び電磁波の進行方向は互いに直角で右手系をなしている。
　この性質は，ここで示した例に限らず，一般的に電磁波に対して成り立つ特徴である。

============================

宇宙開発の現場では、電波を使って通信や制御を行うので電磁波は最も重要な基礎技術の一つ。
Space Japanに掲載されている下記投稿は、電磁気の研究史を紹介し、数学も最新の考え方を使って簡潔に解説している総集編になるので、ご紹介します。

マクスウェル方程式は衛星通信の基本
̶その創出の背景と導出過程̶　飯田尚志（いいだ　たかし）※ 編集顧問
　　※電子情報通信学会フェロー　 独立行政法人宇宙航空研究開発機構理事
http://satcom.jp/84/technicallecturej.pdf

 

この中で、電磁気学の発展が数学の成果を取り入れて実現したことから、数学の重要性を指摘。
イアン・スチュアート，水谷淳訳: “世界を変えた 17 の方程式”　を推奨
　　http://satcom.jp/83/spacejapanbookreviewj.pdf

============================

蛇足　正弦振動だけが波動関数ではない

y=f(x-vt)　の形の関数は、その形を保ったまま進行方向に移動し、波動方程式の条件を満たします。

直線y=x – vt　、放物線　y =(x – vt)^2　、円運動の　y = sin(x – vt )　も波動方程式に該当します。

これと、波は重ね合わせができることを組み合わせると、矩形波や衝撃波などどんな波形でもいろいろな周波数の波の合成で近似できることになりフーリエ級数が成り立ちます。

数学者のイアン・スチュアート氏が厳選した「世界を変えた１７の方程式」には、
１．幾何学と数学がつながったピタゴラスの定理（３平方の定理）
２．ニュートン力学　万有引力、微分積分、　F＝ｍα　など、物の動きと力の関係が明らかに
３．複素数　複素平面とオイラーの公式で円運動や振動を簡潔に理解可能にした
４．電磁気のマックスウェル方程式　電気と磁気の法則を明らかにし、光も電磁波と予言
５．波動方程式　　弦の振動だけでなく、衝撃波など、伝わるもの全てを明らかにした
６．フーリエ変換　レコード・音楽・音声・ラジオやテレビが可能になった
７．ナビエ・ストークスの定理　流体の運動を明らかにした　飛行機の設計もこれで
８．特殊相対性理論　Ｅ ＝　ｍｃ＾２　エネルギーと質量が等価と核エネルギーを解明

などがあります。

 

【図解】アンテナからの電波の発生原理を分かりやすく解説する

　ここには、電荷が電気力線を発し、電荷が動くと電気力線（＝電界）が動き、振動する電荷の電気力線の波が外側に向かって波となって伝わっていくことを示すシミュレーション動画があります。
　横波の電界の変化と同時に直角に磁界の相互誘導が起こり、電界と磁界に直角方向に電磁波となって光の速度の秒速30万Kmで伝わります。

 

小型化する携帯電話とともに進化するアンテナ

　TDKのスマホのアンテナの進化の解説。携帯やスマホは電磁波利用の代表機器です。
　スマホのアンテナは、電波の送信と受信の両方の機能があるようです。

一部を引用ご紹介

携帯電話が電波を送信する時には、信号に対応した電流をアンテナに流します。流すのは、周期的に流れる向きが変わる（プラスとマイナスの入れ替わりが発生する）「交流電流」です。電流の向きが変わる、すなわち電流が時間的な変化をすることにより、アンペールの法則に従って周囲に磁束密度が発生します。発生する磁束密度の大きさも周期的に変化しますので、ファラデーの電磁誘導の法則に従い、磁束密度に応じた強さの電界が発生します。発生した電界の周辺にはさらに磁束密度が発生する、という繰り返しにより、アンテナを起点とした「電磁波」が発生します。

　電磁波を受信する時には、逆にアンテナの周囲にある電磁波によって、アンテナに流れる電流が発生します。これが受信機に伝わり、電波が受信できます。すなわち、アンテナは、電磁波の送信にも受信にも重要な役割を果たすのです。

以下省略