電磁気で交流を考えるとき、基本モデルは円運動の理解と解釈と数式表現と図解です。
なので、ネットで円運動をわかりやすく解説するサイトを探してみたら、
金沢工業大学のサイトが見つかりました。
等速円運動 (uniform circular motion)
その一部をご紹介し、解説を追加させてもらいます。(上をクリックするとリンク先へ)。
物体が円周上を一定の速さで運動しているとき,その運動を 等速円運動 (uniform circular motion) という.
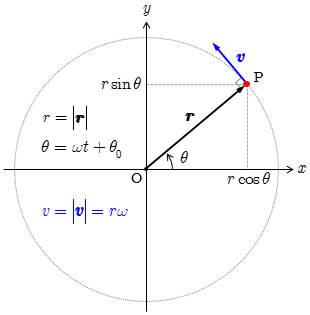
図のように,点 O を中心とする半径 の円周上を一定の速さ で運動する質点の位置を点 P とする.円運動の回転面を 平面にとり,平面の極座標(円座標) , を用いると点 P の位置ベクトルは
– – – (1)
と表せる. は 軸を基準の方向として測ったベクトル の角度であり,点 P が円周上を回転しているので時間とともに変化する回転角を表す.
質点は一定の速さで回転していることから,回転角 の時間変化率(単位時間当たりの回転角)を表す角速度 (angular velocity) は
ω=d/dt=const (一定)ーーー(2)
であり,時刻 で回転角 とすると,式(2)を時間で積分することにより
– – – (3)
を得る.したがって,式(1)の各成分は
,
– – – (4)
と表される.三角関数の角度部分 を 位相 (phase) といい,時刻 での位相 を 初期位相 (initial phase) という
<引用終わり>
上記の説明には、円運動を表す方法には、P(r、)という極座標で表現する方法が紹介されています。
rは半径、は回転角で、極座標の場合は角度を半径1の単位円の円周の長さで表します。
回転角は、一回転すると円周の長さ2π(パイ)、半周がπ、4分の1周(=90度、直角)だと1/2πとなります。
x=cos()y=sin()
が最も簡単な円運動の位置をx、y座標で表現したものとなります。
円運動では時間がたつと回転角が進む。1秒で1回転する場合は、1回転の回転角(円周の長さ)=2π(パイ)なので、
=2πt
1秒でω回だけ回転する場合、t秒後の回転角は
=2πωt
になります。波としてみた場合は、ωは周波数(山と谷で一つの波とするときに1秒間にω個の波がある)に相当しますね。
一方、スタートする位置が原点(上記の図の スタート位置 P(r=1、=0))から 0だけ遅れている(戻っている=反時計方向)場合は、
y=sin(ー0)
と表現されます。=0に進んだら、回転角がー0=0(原点相当位置)になるわけです。
これをまとめ、k回転分遅れ位置からスタートし、t秒後にω回だけ回転したときの
円運動する点Pの高さyは、θo= 2πkと k回転分に変換して2πをまとめて外に出して
y=sin(2π(ωtーk))
これで、だいぶ世の中の波の数式に近づきました。
この式の形を、一般論として図を平行移動させる方法としての表現方法と組み合わせます。
y=f( x )をxy座標面に書いた図に対して、
y=f( x – k )は、図の形をそのままにx軸でkだけ右側に平行移動したものになります。
なので
y=sin( t – x ) は、関数sinの高さyを、回転角を表す時間tと、スタート位置での回転角のずれxで表現したもの。
次に説明する式では、回転角の中に、角度が時間tと位置xで表される式が入ってきます。
波が、空間の中を時間と共に進んでいくので、このような表現になるわけです。
波の要素には、時間と、位置と、高さがあるので、まとめて一つの数式で表現します。
イメージでわかりやすいものを探したら下記に紹介する説明がありました。このグラフをしみじみ眺めると、波とその数学的表現の意味が感じられるようになりそうですね。
受験の味方 https://juken-mikata.net/how-to/physics/wave-equation.html
高校の物理学では、波を表す関数としてy=sin(t-x)を習います。
y=sin(t-x)は曲面を使ったグラフで表されます。



