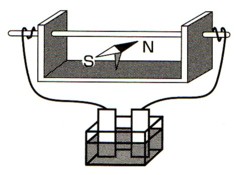
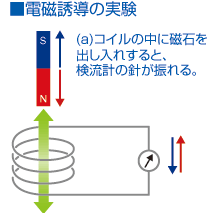
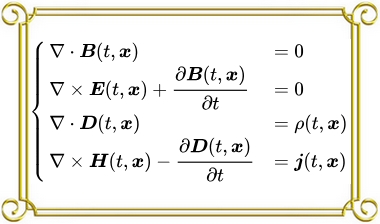誘導加熱式電気炉が、直接電気を通すわけではない炉内の金属を加熱できる仕組みが電磁誘導。
歴史的に、理学系は「電場・磁場」、工学系が「電界・磁界」使用もほぼ同じものです(係数の違いのみ)。
日本の電磁気学の泰斗である砂川重信の古典的名著「電磁気学の考え方」に
1.現代の電磁気学は近接作用説
2.主役は空間に存在する電場と磁場という物理量
3.電場と磁場はマクスウェルの方程式(微分形が本質)に従う
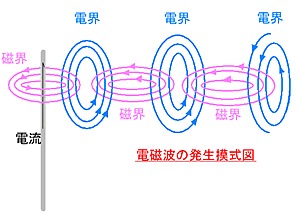
時間で変化する電場と磁場の相互作用で伝わる代表選手が「電波」です。
電波の発生器でありかつ、受信機でもあるアンテナは、電磁波を学ぶモデルに最適。
電磁気学の基礎 大学の講義から学ぶ場合は
ネットで公開されている講義ノートがあります。
兵庫県立大学 理学部 物質科学科 石川 潔
https://www.sci.u-hyogo.ac.jp/material/photo_phys/ishikawa/Class/EM3/EMtext.pdf
式が多く、難解ではありますが、含蓄多くこの講義が理解できると電磁気の関係の全貌が理解できそう。
基本は、これだけ。学問は、高等になるほど簡潔に!
Maxwellの方程式 (twitter投稿のjpg引用紹介
https://twitter.com/tia223joketweet/status/1618783639592120323)

上記の式、上から順に
アンペール・マクスウェルの法則: 「電流」と、「電界の時間変化」は、右ネジ渦磁界を作る
電磁誘導: 磁界の時間変化は、磁界変化を妨げる渦電界を作る
磁界に湧き出しなし
電界の湧き出し量は、中の電荷量と同じ
<演算子>
∂/∂t: 時間微分演算子(時間で微分)
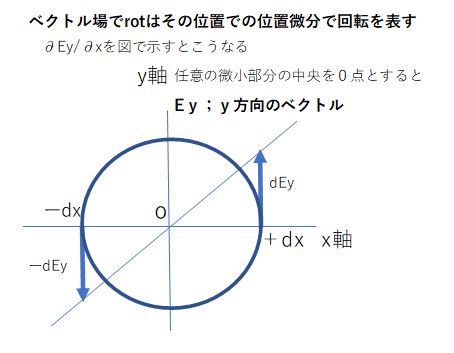
rot: ベクトル場の渦成分を計算する演算子(位置で微分)
div: ベクトル場の湧き出し(発散・スカラー量)を計算する演算子(位置で微分)
電磁波は、位置と時刻が関係する場で起こる現象なので、位置と時刻が変数として登場。
特定の時刻で、湧き出しのないベクトル(div=0)に位置方向での変化rotがあれば渦が発生している。
∂/∂tでは、特定の位置で時間変化が解る。
電波・電磁波とは
真空中では電気も電流もないから、上記のマクスウェルの式は
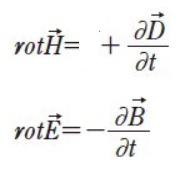
第1式 電界の変化(時間微分)は 垂直方向の渦磁界(磁界のゆがみ・傾き)をつくる
第2式 磁界の変化(時間微分)は 垂直方向の渦電界(電界のゆがみ・傾き)をつくる
ここで間違えやすいのが、電場sinの時間変化(微分)が磁界を作る(=間違いの始まり)なら磁界はcosで位相が90度ずれるのでは?だが、実は時間変化する電場が作る磁場は同位相となるのだと。
右側の時間微分は時間とともに増減する割合で、左側は磁界の位置微分で位置による変化割合。
左辺のrotは、ベクトルの位置微分です。向きと大きさがあるベクトルが位置で変化するということは、微小部分の中心のベクトルから左右のベクトルを見ると左右で方向が逆転していることになる。これって、渦が巻いてる状況なのです。
第1式で、電界sinの時間微分の磁界は cos(90度進む=位相差)になる?
とはならずに、電界も磁界も同相(sin)なのだという。
電場の変化が作るのは磁界ではなく磁界の渦なのだ。
こうなる理由は時間変化とベクトルの渦の微積分の知識と理解が必要で、解説例少なく、
例えばEMANの「電磁波」がある。
電磁波は、実験事実より波であることが解っている。
ポイントは、右辺は時間微分で、左辺は場のベクトルのゆがみ(位置微分)を表していること。そして波は時間と位置に相互の関係がある。
z方向に進行する波は一般的には、F(z-ct)+G(z+ct) であらわされる。
この式の意味を理解しやすいように y=x と y=x-a のグラフで考えてみよう。
xy平面では、傾き45度の直線 y=x
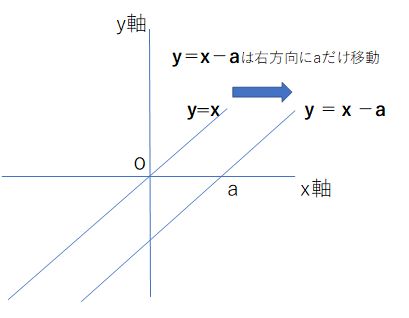
これが x方向に進む波を考えるために a=ct と置けば y=x-ct になると x=ct で0となりx軸を横切る。時間tが増加すると直線はx軸右方向に速度vで移動する。
時間dtの経過で直線のx軸上の移動は dx=cdt の関係がある。
位置のxと時間tとは波の速度vを介して次元が同じとなる。
イメージでわかりやすいものを探したら下記に紹介する説明がありました。このグラフをしみじみ眺めると、波とその数学的表現の意味が感じられるようになりそうですね。
下記のグラフを眺めると、時間と空間位置(進行方向)とが波に関しては同じ効果・影響を持つように見えます。
同じ時刻で進行方向の波を見る時と、同じ位置で時間が変化するときと、波の形は同じようだ。時刻と位置が同等の意味を持ってる!
受験の味方 https://juken-mikata.net/how-to/physics/wave-equation.html
高校の物理学では、波を表す関数としてy=sin(t-x)を習います。
y=sin(t-x)は曲面を使ったグラフで表されます。

電磁波の性質(進行方向には成分がない横波で、磁界と電界は相互に直交)を考慮し簡単のために波の速度がcを使い
Ex=sin(z-ct) とする
第2式の右辺を時間で積分すれば磁場が求められることに着目し、左右入れ替えると
∂B/∂t= ーrotE
電磁波の性質を考慮した条件で整理するとベクトルのx、y、z成分のy成分1項を除きゼロになる。
整理すると
(rotE)x=0
(rotE)y=∂Ex/∂z
= ∂/∂z(sin(z-ct))
=cos(z-ct)
(rotE)z=0
∂B/∂t= ーrotE の結果は、ベクトル成分x、y、zの下記のy成分だけが残る
(∂B/∂t)y=ーcos(z-ct)
時間で微分したものの元の値を求めるには積分すればよい、積分定数(静磁場)を無視すれば
結果として
By = 1/c・sin(z-ct)
もう一つの見方では、任意の定数をkとすると、進行方向でzーct=k となるExは時間経緯とともに移動する。
ctを右辺に移すと
z=ct+k
その微分形(微小変化)は dz=cdt となる
∂B/∂t= ーrotE (ベクトルでx、y、z成分がある)
(∂B/∂t)y=ー∂Ex/∂z (上の式を計算するとy成分だけ値がある)
=ー∂Ex/(c∂t)
=ー1/c・∂Ex/∂t
となるから、
(∂B/∂t)y= ー1/c・∂Ex/∂t
任意のzーct=kでこれがなりたつ。
時間変化で磁界の変化を妨げる電界が発生し、その増減はBとEの変化率が係数と符号が異なるだけで同じということで、同相であることを意味している。
、
位置微分(rot)の結果が時間微分(∂/∂t)でも表現でき、左右の式が係数以外は同じということは、左辺と右辺は波としては同相ということ。
以下、emanの解説を引用し、物理的な意味を考察する。
EMANの電磁波の解説で最も重要な部分を引用でご紹介。
https://eman-physics.net/electromag/wave.html
電場と磁場の波
以前に電場の変化が磁場を生み,磁場の変化が電場を生み出すという説明をした.そしてこの影響が何もない空間を伝わってゆく現象がすなわち電磁波であるとも言った.
しかし,この説明はあまりに定性的なものであって,これだけでは具体的にその波の形がどのようなものになるのかについての正確な形を思い描くことは出来ない.
そこでこれからマクスウェルの方程式から電磁波の存在を導いてみることにしよう.面倒な話は前回済ませたので煩わされることなく計算に入ることができる.
電波と磁波の関係
ここまで電場の波と磁場の波を別々に扱ってきたが,これらの間には関係がある.
それを導くための計算を簡単に済ますために,波の進行方向をZ軸方向に取ることにしよう.真面目に計算していたらすぐに脳みその計算処理限界を超えてしまう.脳みそはなるべく楽な方法を考えるために使うのがよい.
また,上の議論で電場の変化の方向が進行方向と垂直な面内にしかないことが分かったので電場の振幅の方向をx軸方向に取ることにする.こうすることで電磁波の電場成分は次のように簡単に表せることになる
.
それでは準備が整ったところで計算を始めよう.電場と磁場の関係を表した式であるファラデーの法則を使う.
このままでは使いにくいので 3 つの成分に分解した形に書いておこう.
ここに先ほどの電場の波動方程式の解である (2) 式を代入すると,ほとんどの項が 0 になり,2 番目の式ののみ計算すればよいことになる.そして次のような結果となる.
これをtで積分してやれば磁場の形が求められるが,このときに現れる積分定数は静磁場が重なっていても構わないことを表すだけなので無視してよい.よって磁場にはy軸成分しかないことが分かり,その形は
である.
驚いたことに,電場と磁場は,定数である光速度cがかかっているだけの違いがあるだけであり,全く同じ形で伝わっていくのである.前にした定性的な説明では電場と磁場は交互に発生して伝わってゆくというイメージを思い浮かべるかも知れないが,実際には一緒になって伝わってゆくと言った方がよい.
さらにこの結果の式から磁場は電場に対して垂直な方向の成分しか持たない事が分かる.電場を表すベクトルを磁場を表すベクトルの方向に回したとき,右ネジの進む方向が電磁波の進む向きになっている.この事実はz軸とは反対方向に進む波を表している第 2 項の符号がマイナスになっているところにも表れている.
(引用終わり)
ここで紹介されている考え方を解説すると
1.電磁波は電界と磁界が直交する横波で進行方向成分を持たない。進行方向をz方向として電場のx軸成分を Ex=sin(z-ct)とする。
2.上記の前提を入れると第2式では、多くの項が消滅し結果は
rotE+∂By/∂t=0 は、
∂Ex/∂z+∂By/∂t=0 となる。
任意の位置・時刻で電界の位置微分と磁界の時間微分合計が0になる(打ち消しあう)ことになり、変化の仕方は相互に同一同相で符号反対を意味している。
マックスウェル・アンペールの方程式の物理的な意味
第1式は、 電界の時間変化は、同じ大きさの磁界の渦を作る
第2式は、 磁界の時間変化は、同じ大きさで方向反対の電界の渦を作る
これは、電界も磁界も変化の仕方が同じで同相であることを意味している。
電界も磁界もベクトルで大きさがあるが、渦はそれらと異なる。イメージは流れの中に生まれる渦で、中心軸の周りに始めも終わりもない回転が発生した状況。回転するコマが近い。
右辺の時間微分の絶対値が最大値になるところで、左辺の位置微分rotも絶対値が最大になる。
電界がsinなら右辺の時間微分の最大値(傾斜)は時刻0原点0だから、左辺の位置微分の傾き(=渦)最大も時刻0原点0で発生する。
時間微分∂/∂t と位置微分rot の値が一致(符号別にして)とは一方がsinなら片方もsin。
電場の渦は、導体を円周に配置するとその周回積分値を電圧として取り出すことができる(発電機やコイルの逆起電力)。
しかし、磁場の渦から磁界の周回積分値を取り出す方法はなさそう。
電場の波は同時に磁場の波を作り、できた磁場の波は同時に電場の波を作る。
これが、電波の正体で、真空中を伝わる仕組みのようです。
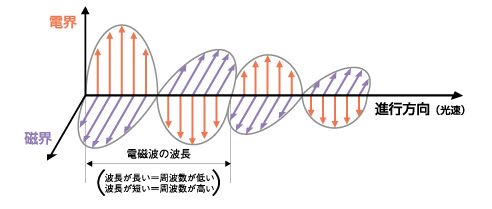 図は 一般社団法人電波産業会 電磁環境委員会 くらしの中の電波 https://www.arib-emf.org/01denpa/denpa01-02.html より引用
図は 一般社団法人電波産業会 電磁環境委員会 くらしの中の電波 https://www.arib-emf.org/01denpa/denpa01-02.html より引用
youtubeで学ぶ 「アンテナの仕組みとは?」
https://www.youtube.com/watch?v=RwT0uOx_aww
2019/08/28
アンテナは電気通信の分野で幅広く使用されており、この動画シリーズではこれと関連した多くのアプリケーションを解説して来ました。アンテナは電磁波を受信して電気信号に変換したり、その逆に電気信号を受信して電磁波として発信します。今回の動画では、アンテナのバックグラウンドにある科学について深掘りしていきます。
スマホも電波を発信し、受信することで通信を実現。現代人の必要知識ですね。
電波発信するアンテナの原理は、電気双極子(+とーの電荷を持つ一対)が入れ代わり続けると、電気双極子で生成し消滅し逆転し続ける電界の変化が同時に直角方向の磁界の変化を生成し、生まれた変化する磁界は直角方向に変化する電界を生成するため、相互に影響しあって進行方向に直角で、電界とそれに直角な磁界の横波を作り光速で伝播すること。
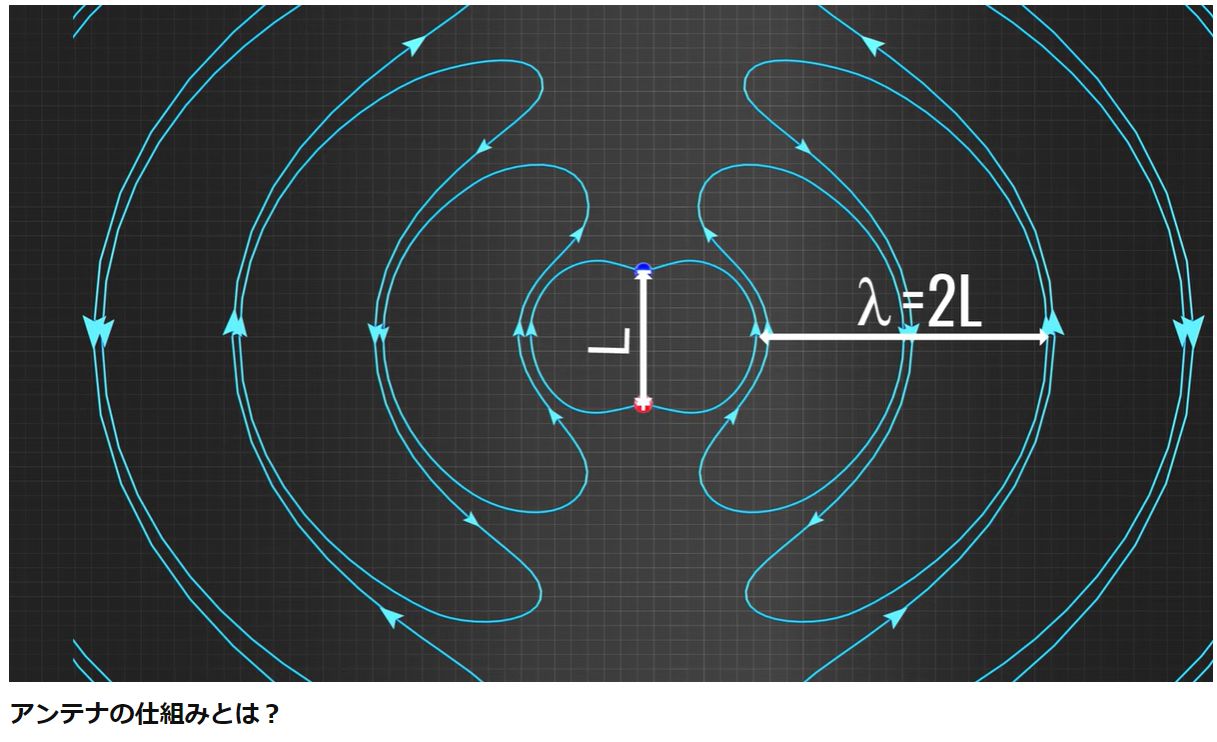
入れ替わる電気双極子を作る方法(下記サイトから部分引用紹介)
https://www.circuitdesign.jp/technical/antenna-s/
アンテナは使用する波長λ(周波数)によってその大きさ(長さ)が決まります。
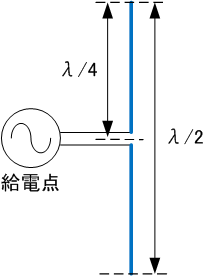
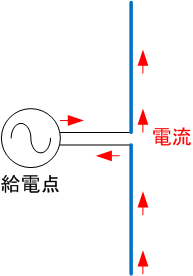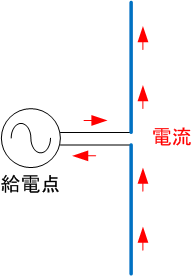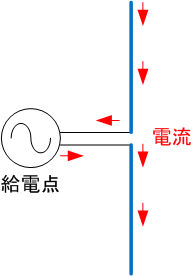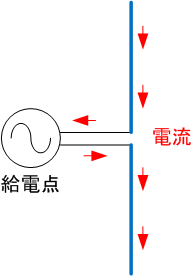
例えば429[MHz]の場合、波長λは約70[cm]で半波長ダイポールアンテナの長さは波長λの半分の約35[cm]になります。左図のように給電点からλ/4ずつの長さ(約17[cm])にした時に、送信の場合はアンテナと送信電波が共振して最大電力を放射し、受信の場合は受信電波とアンテナが共振して最大電力を受けることができます。アンテナを短くしたり曲げたりした場合、共振する周波数がずれてしまうため十分な性能を発揮できなくなります。
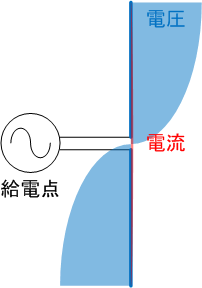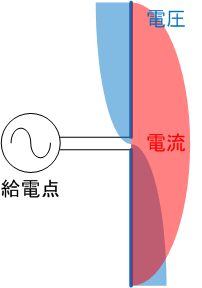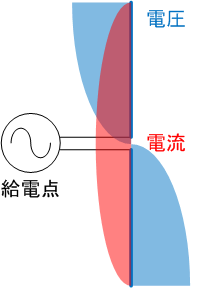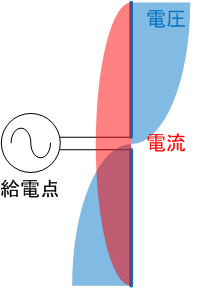
アンテナに発生する電流はアンテナ端で最小となり、真ん中の給電点で最大となります。逆に電圧はアンテナ端で最大、給電点で最小となります。そのため、特にアンテナ端はできる限り金属物を避ける必要があります。
発生した交互に方向逆転する電界は、同時に電磁誘導で交互に逆転する磁界を作り、同時に磁界が電界を作ることで、相互に作用しあって電界と磁界の波が外側に広がってゆく
電流と磁石の相互作用が発見されたのを理論にしたマクスウェルは、電場が磁場を作り、発生した磁場が電場を作ることから電磁波を予言。以下にこの電気と磁気の発見と解明の歴史を解説したサイトを引用でご紹介。
ミカド:電波の歴史~①えっ!光も熱も電磁波なの?マックスウェルの大予言
https://mikado-denso.com/m-online/post-6209
(「電波の歴史」全記事はこちら)
電気と磁気の関連がわかった19世紀前半の軌跡
電波は空間を伝わる電気エネルギーの波です。電池がなくてもゲルマニウムラジオが聞こえるのは、放送局が出した電気エネルギーを受け取っているからです。
皆さんは学校の頃に習ったエルステッドの実験を覚えていますか?デンマークの物理学者ハンス・クリスチャン・エルステッドは、ボルタ電池を使って電流の実験をしていたときに、導線に電流が流れると、近くに置いた方位磁石が振れることを見つけ、電気を流すと周囲の環境が磁気を帯びること発見しました。(1820年)
エルステッドの実験結果は注目を浴びて各地に伝わり、それに強い関心を抱いたフランスのアンペールはわずか2週間で追試に成功し、やがて、電流とそのまわりにできる磁場との関係を表したアンペールの法則を発表しました。(1820年)
一方、エルステッドの実験結果を知ったイギリスのマイケル・ファラデーは、「電流が磁場をつくるなら、その逆も成り立つでは?」と考えて実験を行い、コイルの中に磁石を出し入れすると銅線に電流が流れることを発見して電磁誘導の法則を導き出しました。(1831年)
これらの成果により、今まで別なものと とらえられていた電気と磁気は相互に密接な関連があることが明らかになったのです。
電波はなぜ伝わるの?電波が伝わるしくみ
帯電している空間を電場といい、帯磁している空間を磁場と言いますが、二人の実験により「電場は磁場をつくり、磁場は電場をつくる」ことがわかりました。(電場・磁場はそれぞれ電界・磁界ともいいます)
その理論を基に簡単に説明すると、導体に電流が流れると周囲に磁場をつくり、今度はその磁場が周囲に電場をつくり、それが無限に繰り返されながら空間を伝わっていく波が電波ということになります。
電場と磁場が交互に生み出されて次の波をつくっていくのが電波が伝わるしくみだったのです。
電波は波ですから実際には山と谷があります。
また、電気の波と磁気の波は振幅の方向を直角に取りながら一緒に進んで行きます。その様子を模式化したのが以下の動画です。
マックスウェルが予言した「電磁波の存在」
これらの動作を理論化し、方程式にしたのがイギリスのマックスウェルです。
マックスウェルは小さい頃から数学の才能に富み、20代前半で土星の環の正体を数学的に解明したり、世界で初めてカラー写真の撮影に成功したり、同年に気体の分子運動論を発表していますが、その数年後にアンペールの法則やファラデイの法則等から電気と磁気の性質を次のようにまとめました。
(1)1種類の電荷の力は放射状に直線的に広がる。(ガウスの法則)
(2) 磁気の力はループ状につながっている。(ガウスの法則)
(3) 電気が変化すると磁気が生まれる。(アンペールの法則)
(4) 磁気が変化すると電気が生まれる。(ファラデイの法則)
そしてそれらを方程式にして王立学会で発表しました。(1864年)
マックスウェルは電気と磁気を理論的に融合させた人物として、ニュートンやアインシュタインと並び称される物理学者ですが、現代につながる最大の功績は電磁波の存在を推測したことです。
電磁波というのは電気と磁気を一緒に変化させるエネルギーの波の総称で、今回のテーマである電波はもちろんのこと、レントゲンのX線も電子レンジのマイクロ波もすべて含まれます。
マックスウェルはこの研究を通して、真空や物質中を伝わる電気+磁気の波動(電磁波)が存在することを予言しました。
また、マックスウェルは自分が導き出した方程式に沿って電気・磁気の力によって伝播する波の速度を求めたところ、当時すでにわかっていた光の速度とほぼ一致することが判明したのです。
これによってマックスウェルは光もまた同じ波の一種ではないかと考え、電磁波が光の速度と同等であることを証明することによって、光=電磁波という原理を証明したのでした。
電波も光も熱も、電磁場から生まれる波はすべて電磁波
現在では電磁場の周期的な変化で起こる波動を電磁波と呼び、電波も光もその仲間です。
また熱があるすべてのものからも赤外線という電磁波が放射されていることもわかっています。
鉄を熱すると段々赤味を帯び、さらに熱するとまぶしく光り始めるのは、発生する電磁波の周波数がどんどん上がって可視光線の帯域に及んだということになりますし、私達のからだも熱を持っているので弱い電磁波(赤外線)を出しており、赤外線カメラなどでもそれを知ることができますよね。
地上に降り注ぐ太陽の熱も赤外線ですし、夜空にまたたく星の光も目に見えるので可視光線の帯域の電磁波です。熱そのものが電磁波というわけではありませんが、放射熱は電磁波を通して伝わるため、物質を介さない熱の伝搬は電磁波が運んでいるといえます。
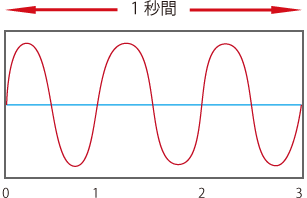
電磁波は「波」なので、海の波のように山と谷がありますが、この波が1秒間に何回通過するかを現した数字が周波数です。単位はHzで表されます。
左の図では1秒間に波の山が3回通過しているので3Hzの電波ということになります。
様々な電磁波を同じ仲間と思えないのは、この周波数(振幅回数)によって性質が大きく変わるからです。
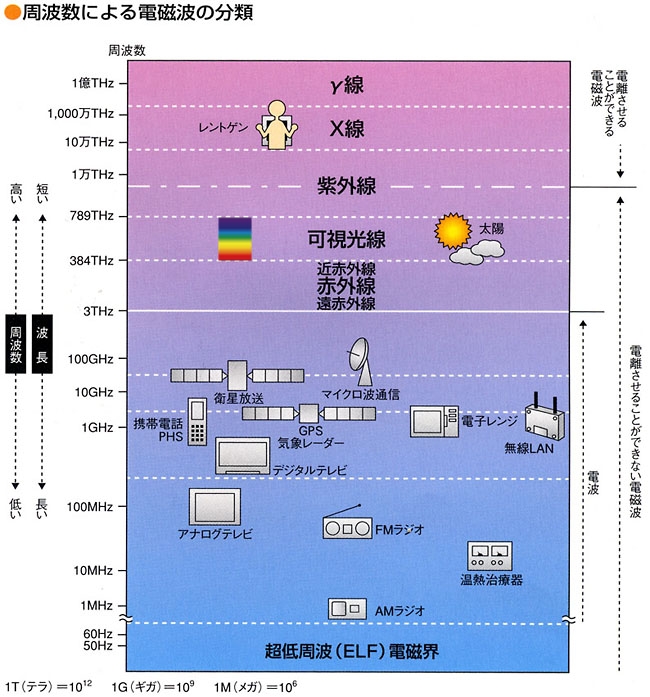
日本の電波法では周波数が300万MHz(=3000GHz=3THz)以下の周波数の電磁波を総称して「電波」と呼んでおり、その帯域外にある赤外線や可視光線は通常電波とはいいませんが、実体が明らかになる前から計算という手法で仮説を導き出し、電磁波というものの存在を予言したマックスウェルは、電磁波理論を完成させた偉大な科学者といわざるを得ません。
上の図は電磁波の周波数による分類表です。電波の周波数は、高くなればなるほど扱える情報量が増えますが、その分直進性が増すため物陰に隠れるとすぐに届かなくなる傾向があります。
電波によく似た波で音波(音)がありますが、音波は空気などの媒質に生ずる波動なので電磁波ではありません。
電波は真空でも伝わりますが、音波は真空では伝わらないため、どんなに宇宙戦艦ヤマトが宇宙空間で敵国相手に派手な戦闘を繰り広げても、実際はなにひとつ物音がしないのです。
現在は、電波(電磁波)に関して様々な事柄がわかっていますが、マックスウェルが仮説を立てた「電磁波の存在」が実証されるのは、それから30数年後です。
マックスウェルの方程式は複雑で難解なものだったため、数学がそれほど重要でなかった当時の物理学の世界では、いまよりも評価が低かったそうです。
ですが、ノストラダムスの大予言はハズれても、計算と数式から電磁波の存在を予測したマックスウェルの予言は、まさに「大予言」だったといえるでしょう。
理論上の仮説だった「電磁波の存在」を実際に実験で証明したのは、ドイツの物理学者ハインリッヒ・ヘルツでした。次回はヘルツについてのヒストリーをお届けします。
(➡ 次回:②電波を発見しても電波の価値は見いだせなかったヘルツ)