現代の鋳造では、金属の溶解には、
1.燃焼熱(炭・石炭・コークス・ガス)
2.電気炉(抵抗発熱・電磁誘導電流による加熱・アーク放電)
3.熱線(太陽光などをレンズ利用して集中させる)
が利用されますが、銑鉄や銅合金などの高温溶解必要な工業用鋳造では、誘導加熱電気炉がよく利用されます。
電気誘導加熱式電気炉は、コイルに電流を流すと、コイル内部に磁場が発生。交流を流すと電流の反転するたびに磁場が反転しそれによって誘導電流が発生して発熱することを利用。
誘導電流が、炉に投入した金属材料に効率よく発生するように交流サイクルを調整する必要があります。また、高エネルギーを投入するため特別高圧電源から大電流にするために変圧し、さらに最適なサイクルとするためにコンバーター・インバーターが用いられ、その過程で発生する高調波を吸収するための装置なども必要になります。
電気のイメージには、電気の1単位C(クーロン)同士が1mで働きあう力がどれくらい大きいかを知ると、そのすさまじさで実感できます。
プラスの電荷1Cとマイナスの電荷1Cが1mの距離で相対した時に働く引力F=9x10の9乗N=9x10の8乗KgW=9x10の5乗tW=90万トン重。
雷雲で離れた雲と地上とで雷が発生するのもなるほどです。
下敷きをこすったら頭の髪の毛が逆立つのは、重力より大きな力がはたくことを意味しています。
なので、電気を貯めるコンデンサーの単位は、
μ(マイクロ 10のー6乗)、n(ナノ 10のー9乗)、p(ピコ 10のー12乗)が使われます。
日本では「nF(ナノファラッド)」が使われることはまれで、1nFのかわりに0.001μFあるいは1000pFと表記するのが一般的と。
電磁気の単位系は、歴史的な経緯から、MKSA単位系・CGS単位系・Gauss単位系があり、困惑させられる。
相互の関係は 例えばこちらを参照
広島大学「電磁気学における単位系」 https://home.hiroshima-u.ac.jp/kyam/pages/results/monograph/Ref01_unit43W.pdf
電磁気の基礎を学ぼう
電磁気は、熱源以外にもモーターや制御系でも利用されますが、機械系は電気はよく分からないという人が多い。
そこで、電磁気学の基礎を復習しましょう。
電気も磁気も目に見えません。空間中に分布するその量と変化の影響は Maxwellの方程式で正確に表現できるそうです。
方程式は、ベクトルの偏微分で、内積と外積で表現されています。
電気とは
原子核のまわりをまわっている電子が原子核のまわりの軌道から飛び出したものを自由電子
電子が持っている電気を「電荷」 クーロン(単位C) q Q
電荷の流れを「電流」 I アンペア 単位(A =C/sec 毎秒流れる電気量)
電気を流そうとする力の差が「電圧」 ボルト V
電気の流れを妨げる大きさが「抵抗」 R
電圧と電流と抵抗の関係 V=IxR
電力(W)=電圧(V)×電流(A) 電気がする時間(秒)当たりの仕事を表す単位がワット。
直流と交流 電気が一方向にだけ流れるのが直流DC、 周期的に変化するのが交流AC
電流と磁界
電流が流れる導線の周囲には、それを取り囲む磁界が発生する。 磁界の向きは、レンツの右手の法則
わかりやすい解説がこれ、
https://www.chuo-tky.ed.jp/~ginza-jh/_resources/content/10001/20200428-135558.pdf
電磁気学の基本:マクスウェル方程式とその意味
記号と意味
| C | 電荷 (クーロン) |
| J | 電流密度 :ベクトル。単位はC/m2 |
| ρ | 電荷密度: (ギリシア文字のロー)。単位は C/m3 単位体積あたりの電荷。 |
| D | 電束密度:ベクトル。単位は C/m2 で方向と大きさを持つ |
| E | 電場ベクトル:(ベクトル) 単位は N/m2(平米当たりニュートン) |
| B | 磁束密度:ベクトル。単位は Wb/m2≡T(テスラ) で方向と大きさを持つ |
| H | 磁場ベクトル:H 単位は N/Wb( ニュートン / ウェーバ ) |
磁荷: 単位はWb(ウェーバ)
磁荷密度は「ゼロ」
マクスウェル方程式の (1) 式の対応で (2) 式をみると,「磁荷密度」の項がゼロになっていることに気づく。このことを以下のように表現する。
“磁荷” は単独では存在しない。あるいは,磁気単極子は存在しない。磁石のN(正)極,S(負)極は単独で現れることはなく,必ず対になって現れる。

マクスウェル方程式の逆三角形の演算子は、ナブラとよみます(下に解説引用紹介)。
ナブラ演算子には、スカラーと内積と外積の3つの作用のさせ方があります。
内積は、逆三角形・ベクトル :スカラー 物理的には湧き出しの有無
外積は、逆三角形xベクトル :ベクトル 物理的には状態が回転(渦など)であることを表現
マクスウェル方程式の意味は、
(3)は、(磁束密度Bの時間変化)を相殺する回転電場が発生する。これにより誘導電流(渦電流)が発生。
(4)は、電流周りに(電流密度 J +(電流密度Dの時間変化))に相当する、回転磁場が発生する。電流をコイルにすることでコイル(電炉)の内側に大きな磁束が発生。
数学と物理学の相互利用
数学でのナブラ演算子の作用のさせ方である スカラー・ベクトルの内積・外積 を物理現象の説明に使えることに気が付いた人たちがいました。
流体モデルでは、
ナブラ演算子の内積は、流体が指定空間から流れ出す量の総量なので、湧き出し(発散div)といいます。(通常は物理量不変なので出入り合計=ゼロ)。
ナブラ演算子の外積は、コマがZ軸を軸に反時計周りで回転がモデル。x軸上では原点から離れるとy方向に速度Up,y軸上では原点から離れるとーx方向に速度Up,z軸の方向にはどこでも速度0
外積の計算式に当てはめると、スカラー量がプラスでベクトルの向きはz軸のプラス方向になります。
下記引用の「ナブラだけを分離する」に詳しい解説あり。
http://www.iwata-system-support.com/CAE_HomePage/vector/vectana11/vectana11.html


ベクトル演算(和・差・内積・外積)の基礎
ベクトルとベクトルの演算では、加算減算と内積と外積というのがあります。
加算は、ベクトルとベクトルの合成になります。減算は方向を逆転させた合成。
イメージするには、単位ベクトルからスタート
単位ベクトル=大きさが1で、x、y、z軸それぞれで原点から1の距離。
内積=スカラー量(方向がなく大きさだけ)になり、計算方法は
同じ(x、y、z)成分同士の積の和、
同じベクトルの内積は線の長さの2乗。直交する2本のベクトルではゼロ。
イメージ的には、
x軸上の1=3次元座標で、(1,0,0)と(1,0,0)では、1
計算式 1*1+0*0+0*0=1
x軸上の1,y軸上の1 (1,0,0)と(0,1,0)では、0。
計算式 1*0+0*1+0*0=0
外積=二つのベクトルがつくるひし形に垂直でベクトル1から2に右手の指が回るとき右手の親指方向で、ひし形面積の大きさのベクトル
二つのベクトルがx軸とy軸なら、方向はz軸(プラス方向)で、大きさが面積のベクトル

これをわかりやすく解説したサイトを下記に部分引用でご紹介します。
https://eman-physics.net/math/vector02.html
ナブラだけを分離する
前回,関数の傾きを表すベクトルとして
というものを定義した.この
のことを関数
の「勾配」または「グラーディエント」と呼ぶのであった.また,ここで使っている
という記号は単独では「ナブラ」と呼ぶのであった.
さて,このナブラだけをグラーディエントから切り離して,次のようなものであると定義してみよう.ここに出てくる
などは本当はこれだけでは意味がないのだが,「この後ろに来るものに対して偏微分を行う」という意味の記号として受け入れることにしよう.このように,他のものに対して計算の指示を与える記号を「演算子」と呼ぶ.このようなものを導入することで数式の表現に幅が広がるのである.
普段あまり意識していないが「+」「-」「×」「÷」などの記号も広い意味での演算子である.だからなどを他の演算子と区別する必要があるときには「微分演算子」と呼ぶ.ナブラもまた微分演算子であるが,区別する必要があれば「ベクトル微分演算子」とでも呼んでおけばいいだろう.
演算子を働かせて対象を操作することを「(演算子を)作用させる」と表現する.英語では operate という動詞を使うので「オペレートする」ということもある.数学では演算子 (operator) のことを「作用素」と呼んでいるので数学寄りの教科書を読むときに困惑しないようにしよう.この辺り,物理では翻訳に一貫性がないな.
ベクトルの湧き出し
さて,ナブラだけを分離すると何が出来るというのか?例えば,とベクトル
との内積を作ってみると次のようになる.
と
との内積を作ること自体には理由などない.ただ内積の計算ルールに倣ってこのように定義してみましょう,というだけのことだ.ところがなんと,この右辺の計算内容には意味が見い出せるのである.それをこれから説明していこう.
(1) 式の右辺ではベクトルの位置による変化具合を計算しているらしいことは分かるだろう.この
というのは場所によって値が決まるようなベクトルである.空間に無数のベクトルが張り付いて存在しているようなイメージでとらえても良い.前回の話の最後に説明したが,そういうものをベクトル場と呼ぶのだった.
ベクトルが空間を埋め尽くしている様子を想像してみて欲しい.そのベクトルは微分できるように滑らかに変化しているから,どこかを境にして矢印の方向や大きさが突如として不連続に変わるということはない.だから,それはまるで水の流れを表しているようにも感じられる.ある部分ではベクトルが小さくなっていたり,別の部分では大きくなっていたりすることだろう.それに対して,あたかも空間からベクトルが湧き出してきていたり,空間にベクトルが徐々に吸い込まれて消えてしまっているような空想を当てはめてみる.(1) 式の右辺は,そのような空間の各点におけるベクトルの湧き出しや吸い込みの度合いをプラスマイナスの値として算出していることに相当するのである.
なぜそう言えるのだろうか?(1) 式の右辺の第 1 項を見てみよう.これが正の値だとすると,軸の正の方向に目をやるにつれて
が増加していることになる.ベクトルを水の流れのようなイメージでとらえると,
軸の正の方向に流れる水の流れがどんどん増しているようなものであり,どこか途中に湧き水があるに違いないというイメージになる.
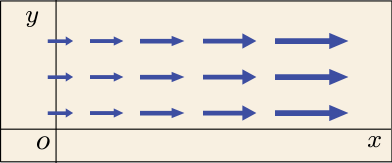
もし第 1 項が負になっていたとしても,代わりに第 2 項や第 3 項が正の値で全体として 0 だったならば,もともと方向に向かっていた水の流れが
方向や
方向に向きを変えただけで全体としては湧き水があったわけではないのだな,などと解釈できる.
イメージを正しく理解してもらうためにはもう少し色々と説明が必要な気もするが,ここでは式の定義と計算法を分かってもらうのが第一目標なので,軽めの説明で済ませることにしよう.まだ説明が足りないことと言えば・・・,例えば次の図のような場合も第 1 項は正なのである.
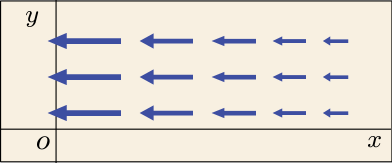
右に目をやるにつれてベクトルは小さくなっているが,これらのベクトルの成分がもともと負だったものが増加していっているために,絶対値が減少しているように見えるだけである.しかしイメージとしては左へ向かって流れる水流が増加しているようであり,途中に湧き出しがあるというイメージは変わらず成り立っていることになる.
このように,水流が右へ流れるか,左へ流れるか,それ以外のどちらへ流れているかに関係なく,が正ならばその地点では水の湧き出しがあり,水量が増加していることを意味しているのである.
もう少しだけ数量的な説明を知りたければずっと前に書いた記事があるのでそちらも参考にしてもらいたい.そこでは電磁気学で使う「ガウスの定理」というものの説明が主題になっていて,まだ説明していないベクトルの積分がいきなり出てくるのだが,そこは軽く読み飛ばしてもらったらいいと思う.ベクトルの積分はもう少し後で説明する予定なので,そこまで理解してから読んでもらっても良いだろう.その記事中では ∇・E を div E と表現しているが,それは今回の記事をもう少し先まで読むと分かる.
というわけで,こののことを,ベクトル
の「湧き出し」または「ダイバージェンス」と呼ぶ.
は,空間中の場所ごとで一つの数値が決まるものであり,そういうものを「スカラー場」と呼ぶのであった.
ベクトルの回転
ナブラを分離した効用は他にもある.次はとベクトル
との外積を作ってみる.外積の定義に倣って定義してやると次のようなものが出来上がる.
何と,この右辺の計算内容にも意味が見い出せる.ベクトル場を視覚化してみると,渦を巻いているように見える場所もあることだろう.はっきりとした渦には見えなくとも,もしそこに水車を置いたならば,ベクトルの流れの微妙な差によって回転を始めるのではないかと思える場所が幾つもある.
この (2) 式の右辺はベクトルになっていて 3 つの成分を持つが,例えばその第 1 成分は,回転軸を軸方向に向けて設置された水車を空間中に置いた時にどれくらいの勢いで回転するかを表しているのである.この値が正ならば,
軸の正の向きを向いた時に時計回りに見えるような回転をしているし,負ならば反時計回りをしていることを意味している.他の軸についても同様である.
この (2) 式の右辺のベクトル全体としては,「もし自由に軸の方向を変えられる水車(それは自由に回転できる羽根付きボールのようなものだろうか)があるとすれば,それはどの方向を軸として右回りするか」というのを表していることになる.しかしそのことを示すのはまだ少しレベルが高いのでやめておこう.
念の為に書いておくと,それは,ベクトル場をそのままに座標軸だけを回転したときに,新しい座標で表した ∇×A の方向がそれに応じてどのように回転するかを確かめれば良い.例えば,∇×A が初めにある方向を向いているとして,その方向が新しい x 軸になるような座標変換をしてやる.もしその新しい座標系で計算される新しい ∇×A が新しい x 軸を向いていれば,新しい y 軸や z 軸の周りには渦成分はなくて,ただ x 軸の周りにだけ渦巻いているということになるからだ.つまり,元々の座標においても ∇×A が示す軸の周りにだけ渦成分があったことになる.
というわけで,こののことを,ベクトル
の「回転」または「ローテーション」と呼ぶ.
なぜそんなことが言えるのかを少しだけ説明しておこう.(2) 式の右辺の第 3 成分が分かりやすい.これは水車の回転軸が方向を向くように設置されている場合を示しており,
平面内に生じている回転を意味しているのでイメージしやすいだろう.第 1 項は
である.これが正だとすると,
方向へ進むほどに流れの
成分が強いことになるので,水車の右側の方が強く
方向に押され,
平面を上から見降ろしていると水車は反時計回りに回転を始めることになる.しかし
軸というのは
平面からこちらに向かって伸びているものなので,その方向を向いて眺めれば,水車の回転は時計回りである.
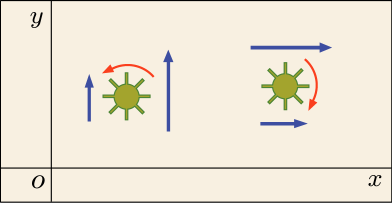
第 2 項にどうしてマイナスがついているのかは,同様にして考えれば分かるだろう.が正の場合,
方向へ行くほど
方向への流れが強いので,水車は上から見降ろして時計回りすることになるからである.これは先ほどとは逆であるからマイナスが付いていることで話が合うのである.
上記の解説で、補足すると、単純化して
Z軸を軸とするコマの回転モデルを考えてみる
Z方向には、速度成分も速度変化も存在しないから、上の(2)式で、zがある演算は全てゼロになり、z軸になる最後の式だけが意味をもつ。
x軸方向でy方向ベクトルの増加(=上方向へ加速)と、y軸方向でx方向ベクトルの減少(=左(ーx)方向へ加速)を足すことになり、上の図の解説の通りとなる。
式が複雑で覚えにくいが、(2)式は、分母(下側)だけを見れば
(x、y、z) → (y-z)(z-x)(x-y)の順番になっていて
分子側は、( )の中の相手分になっているとみれば、案外簡単!


