物理量を工学で扱うときに、流れはベクトルで扱い、その線積分・面積分や、特性を細かく見る偏微分とその合成である積分が使われます。
概念のイメージができると理解しやすくなり、使えるようになります。数式暗記が数学・物理じゃない!
基本はマックスウェル方程式です。いろいろありますが、ここでは電磁現象が場で起こるとする考え方を象徴する微分形で表現した関係式をご紹介。
式に出てくる div は、湧き出しがあるかどうかを調べる演算子です。通常の流体では密閉空間に入る量と出る量は同じなのでゼロとなります。電気の場合は、マイナスの電荷をもつ電子やプラスの電荷をもつ陽子が湧き出しになります。しかし磁気には磁気素子もそれによる湧き出しもなく、電気の動きが磁界を作るが定説になっています。
式に出てくる rot は、場が回転する渦を作っているときに値を持つ演算子です。回転をコマの回転軸方向ベクトルで表現します。隣と速度差・ベクトルの大きさの違いが発生していることを表します。
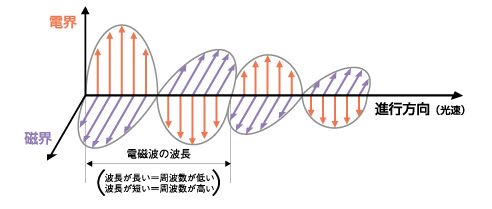
この図の場合は、z方向に進む電磁波は電界と磁界が直行しz方向成分を持たない平面波で、
電界D=(Dx, 0, 0) 磁界B=(0、By, 0)に簡略化できる。
電界 Dx=sin(kzーwt) 磁界 By=sin(kzーwt) のように同相の波動となり、位置微分rotがベクトル場で回転が値を持つケース解説(下図)のCが該当し値を持つ。
上図の場合に、Z方向の位置と時間経過wtが 同じ次元で関係していることは、本質的に重要だ。これにより時間微分と位置微分が同等の意味を持つことになるためだ。
マクスウェル方程式で、電場と磁場の時間による微分変化率とROTによる位置微分変化率が同じだということは、そのまま電場と磁場の変化が同相だということを意味している。
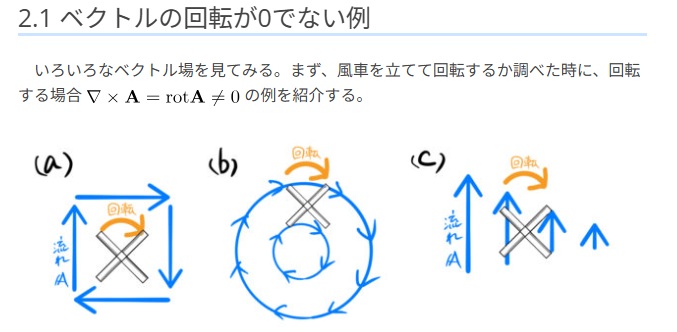
下図は、ベクトル場でROTが値を持ち渦を巻いている例です。図中のXは風車を表し、その軸周囲の流れの速度変化により風車が回ることを示しています。
(a)は偏微分でx軸、y軸で回転がある場合。(b)はコマの回転や直線電流の周りの磁界、 (c)はベクトル場で並行するベクトルに傾向的な差がある場合で電磁波や鳴門の渦潮が該当。大きな流れの中で流れに不均一が発生していると隣り合ったベクトルの大きさの違いで摩擦的に渦要素が発生。鳴門の渦潮はそれにより発生します。
ROTの意味
ベクトル解析における回転 (rot、Curlとも呼ばれます) は、3次元空間のベクトル場 A(x,y,z) の各点における「回転の度合い」を表すベクトル量です。
i,j,kをx、y、z方向の単位ベクトルとすると、
ベクトル場 がで表され
それが、z軸を中心に回転する場合は、z方向成分がなく、z方向の変化もないことを考慮すると、 の計算式は
rotA=(∂Ay/∂x−∂Ax/∂y)k
となりZ軸方向を向く右ねじの回転ベクトル。x軸上ではy方向だけ、y軸上ではx方向だけ、それぞれ原点を中心にすると正負の位置では反対方向を向く、まさに回転ですね。
解りやすくするために、Z軸を中心軸に回転するコマの例では下図のようになります。
電流の周囲にrotでできる磁界の大きさの分布は下記の図がモデルです。
コマの回転では半径増加に比例して速度が増えるのとは違い、電流で発生する磁界では一周線積分が同じ値になるため、大きさは発生源からの距離に反比例します。
注意ポイント: 電流で発生する静磁界の場合は、内部に電流が通っていない部分では、その微分表現である rotB=領域内の電流密度I=0 となり、常にゼロ。
なお、電流は太さのない数学の線ではなく、電線など直径がありその中で均等に電流が流れるために、最大の磁界は電線の表面になるということです(証明は省略)。
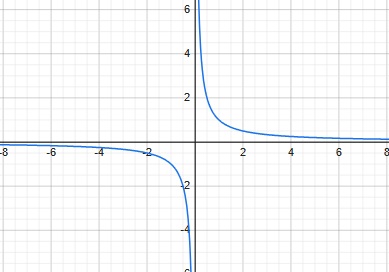
上図を見ると、X軸上の磁界は中心からの距離に反比例するy方向だけになる。
コマの回転の場合は、円周の任意の部分で中心軸を原点とする周回積分は、円周長さが半径に比例し速度も半径に比例するので半径の2乗に比例します。周積分が一定値になる電流による磁界とは異なることが分かります。
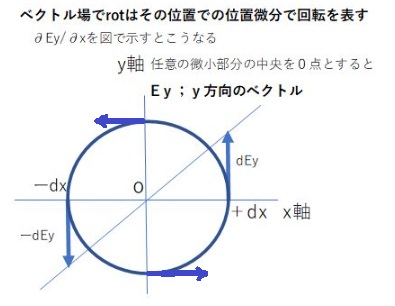
中心軸から見た場合は、 ROTでみると、∂Ay/∂x−∂Ax/∂y で中心の右と上を見ると
Ay=wx Ax=ーwy で、それぞれを偏微分した値は w-(-w)=2wで一定値になり、渦と判定されます。
これだとマクスウェル方程式のrotで渦になるとの理解は分かりやすいのですが、
X軸上では、x方向成分が存在しないのにxが増えるとy方向成分が減少する
x方向に進むとy方向磁界が減少しX軸上のy方向成分では上図のCに相当する。となると、任意の部分で変化するROTが発生してるように感じる。変だぞ!!!
X軸上では、磁界は無限直線電流の周囲にできる Hy=C/x だけで、 Hx=0、 Hz=0 ですね。
こう考えるとx軸上のROTは、 ーC/x2 で、一定値ではなくなります。
そこで、xy平面での磁界を表す式でROTを計算すると、y方向成分による回転とx方向成分による回転が同じ大きさとなり打ち消しあっていることが分かりました。x軸ではx方向磁界が存在しないけどxから少し離れるとx方向成分が発生しているためです。
その解説がGeminiにありましたのでご紹介

上のケースは直線電流の周りの静磁界です。 時間変化がありROTが発生する電磁波とは異なっています
一方、電磁波は、電流がない真空の世界で時間変化する電界と磁界が相互に直角に磁界と電界を作り、光の速度で伝播するというもの。
モデルは、無限遠から飛んでくる電磁波モデルで、Z方向に進行する電磁波は電界がDx成分だけ、磁界By成分だけ、それ以外の成分がない平面波と仮定できる。
無限遠方では平面波として進む電磁波の解説を行っている動画があります。
【大学物理】電磁気学 第42回 – 平面電磁波 https://www.youtube.com/watch?v=bjnMb4iNLNg
時間変化のない直線電流では、電流を含む周囲の磁界は周回積分が電流値となりROTがある渦磁界だが、電流がない部分ではROT=0 で磁界の渦はない。
一方、時間変化で伝播する電波では無限遠では電界と磁界が相互に作りあい伝播しROTが存在する平面波として近似できる。
電磁波は、相互に直角な電界と磁界が同時に相互に影響しあって同相の波として、光速度で伝播します。
それらが、すべてこの短く美しい4つの方程式から導かれるそうです。すごいですね。
http://www.maroon.dti.ne.jp/koten-kairo/works/transistor/Section2/momentum2.htmlから引用でご紹介
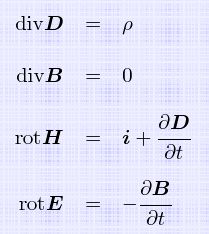
第1式は、電束の湧き出しは電荷密度と同じ(電気素子の存在)で電気素子から球状に広がること、
第2式は磁束には湧き出しがない(磁素はなく)副次的な現象であることを意味。
第3式は、電流と電束の時間微分(時間変化)が渦磁界を作る。電流の方向に回転軸を持つ渦磁界ができる。
周期的に変化する波の場合は時間微分最大(極大値)とはsinなら時間座標の原点、その時磁界の渦が最大(極大値)とは空間での磁界の変化(傾き)最大(=磁界の波が空間でもsinならその原点に相当)となる。
※ 数学的には 右方向に進む波は位置と時間の関数で y=sin(xーt) の形で表される。
※ 渦は方向ベクトルがある点を中心として逆転する現象、コマは軸を中心に左右逆方向に動いて回る。
第4式は磁束の時間微分(時間による変化)が磁束の反対方向の直角な渦電界を生む
第3式と第4式とから、電界の変化が磁界を作り磁界の変化が電界を作ること、その結果電磁波ができ、さらにその速度は測定されていた光速と同じであることが判明し、光も電磁波だと解ったのです。
なお、電流や電束変化電流(変位電流)などの起磁力で生まれた磁界が物質に作用すると、物質特有の原子スピンなどによる磁性関係の特性を呼び起こし物質により1倍から10万倍の磁力が生まれ起電力や電流に力を与える物理量になる磁束を生みます。その変換係数が透磁率μ。
絶縁体2枚の電位差で発生する+-の電気量で発生する電界が、間の物質に作用すると誘電率εにより分極を発生しー+が生まれることで物質内部の電界強度が下がります。磁界を生ずる能力や電流に生ずる力の検討に誘電物質の影響を受けないものとして電束が定義されました。
マックスウェル方程式と光速一定がアインシュタインの特殊相対性理論につながったと
マックスウェル方程式で、電磁気が場のエネルギーや運動量(進行方向)を持つことが導かれ、それに光速一定と、動かない観測者・電子(電流)とともに移動する観測者双方に成り立つ理論を考えてアインシュタインの相対性理論が導かれたのだと。
この問題は、電磁気(電気・電界・磁界)が存在する空間(x、y、z)と時間(t)が関係する4元系。
現代では、それらをさらに数学的にベクトルポテンシャル(電流が作る磁場のポテンシャル)・スカラーポテンシャルとしてまとめて一つの式で表現する考え方ができ、それを簡潔に表す記法ができて(アインシュタインの圧縮記法)、電磁場と電気と電流をまとめて表現できるようになったと。
新しい概念を学ぶには動画が一番 youtube 4本あるマクスウェル方程式を1本にまとめ、相対論的な表式にします. をご紹介
マクスウェル方程式を1本にまとめてみた https://www.youtube.com/watch?v=Yhyvd37Xmjk
電気炉がどうして外側が溶けないのか、を調べていったら、思いがけず現代物理学の最先端(?)を垣間見ることができました。
現代の物理学・工学は
ニュートンが見つけた 力学 F=mα から導かれる 重力以外では、「物が接触し同じ方向にだけ働く」力・加速度・質量・応力など、人類が生きる世界経験を反映した設計の基礎概念
ファラデーが緻密な実験を積み重ねて発見した「空間を通して相互に直角方向に働く」電磁気とその相互作用と、それを法則として定式化し電磁気が電磁波を作り、光と同じだと予言したマックスウェル
さらに光速一定とマックスウェル方程式から場のエネルギー E=mc^2 (質量とエネルギーの関係)を発見したアインシュタイン
それらを駆使してできた現代の電磁気利用の、光通信・ネットワーク・センサーや、核エネルギーなどの多彩な利用や、宇宙への適用拡大。
へとつながっていったのだと。現代の鋳造はそれらすべてを利用していた現場でした。
難解な物理学と数学はさておいて
電磁気学では、わずか4つしかないマクスウェル方程式と、それが力を生む1つのローレンツ力の式しかなく、それだけで基本理解ができてしまいます。さらにマクスウェル方程式は、4つのうちの3・4番目が重要なので、合計3つを使えれば役に立つ。

第3式は、 電流が渦磁界をつくる
第4式は、 磁界の変化が渦電界を作る
ローレンツ力は、電荷が磁界を動くと、動く方向x磁界のベクトルの外積の力を受ける(モーターの原理・右手系)
これらに使われている謎の式が、微分・偏微分rotとベクトルの積なので、その意味を知れば千人力!
| 概念 | 意味や利用方法 |
|---|---|
| ベクトル | 空間で大きさと方向をもつもの 水・油・空気など流体の流れ、重力や押す引くなどの力、電界、磁界などは、ベクトルで表すことができる |
| ベクトルの内積 | ベクトルFとベクトルL の内積は、W=F・L 計算式=|F|x|L|x cosΘ(FとLの絶対値と角度cosの積、角度ΘはFとLの角度)。 力学的には斜面に働く力がその方向に動かしたときの仕事量や、面から流れ出る量を表す。 |
| ベクトルの外積 | ベクトルUとベクトルVの外積は W=UxV 大きさはUとVが作る方形の面積で方向が右手系(親指U 人差し指V 中指W) 電磁気では、磁界を動く電荷が受ける力に使われる F=qv x B (電荷qが速度vで磁界Bを動くに受ける力F) 面積分では、微小面の面積と面の垂線方向を示す微小面積ベクトルとして利用する ※ ベクトルの外積の式1行で、 右手系や左手系が表現できる |
| 微分 | ある現象を細かく分け、分けたものの特徴を調べること。 数学では、xの関数f(x)をxの位置の微小増分dxの時に、f(x)がどれだけ増えるか(=グラフ上の傾き)をいう。 進む方向で増加・減少するかどうか、その大きさなどを調べることができる。 sinを微分するとcosに、cosを微分すると-sinになる(交流電流の基本)。 ※コイルは電流で磁界が発生。電流が時間変化する交流電流では、電流変化で発生する磁界の変化で誘導電界が発生し電流が流れないように働き交流電流の流れを妨害する。このため電流波形の位相は電源電圧より90度遅れる。 電磁気の基本のマクスウェル方程式は、4つの微分方程式で表現される。 |
| 偏微分 | 空間的(3次元)・面積的(布)などで、その位置での関数値を x軸・y軸・z軸に分解してdx、dy、dzでの増分を調べる。 |
| 偏微分:勾配 | gradient(grad)とも言います。その位置の傾きをx、y、z方向成分で表すベクトルになります。 以下の3つの図は 「具体例で学ぶ数学」https://mathwords.net/graddivrot からの引用です。 下記の例では、y=f(x)なら、x、y平面での線の傾きになり、山の高さをz=f(x、y)とすると、山の斜面の傾きになるので「勾配」そのものです。3次元では温度分布をt=f(x、y、z)とすると空間の温度勾配になります。  |
| 偏微分:発散 | divergence(div)とも言います。その位置の微小立体からの湧き出し量を示すスカラー量です。 流れ分析の基礎式で物質不滅(生まれも消えもしない)で通常はゼロになります。  |
| 偏微分:回転 | rotation(rot)とも言います。ベクトルVが渦を巻くときに、微小立体部分の回転の大きさと回転方向を指すベクトルです。 3次元空間(x、y、z)で、z軸を軸として反時計回りに回るコマを考えると、(x、y、z)=(1,0,0)では+y方向に動き、(0,1,0)ではーx方向に動き、z軸方向には動き成分もx方向やy方向の動きの変化もないのが渦の特徴。 そのため、第1項と第2項が共に0となり、第3項だけが残ります。 任意のコマの回転を考えた時に、座標軸の回転や移動で、コマの軸と移動後のz軸を合わせることができるので、この関係は全ての渦に共通な性質だとわかります。 電磁気学では、電流や、電界の変化が作る渦磁界や、磁界の変化が作る渦電界の定義に使います。  |
| 積分 | 細かく分けたものを集めて元の形にする。インテグラルの記号を使う。次元の数だけ並べて使う。1つなら1次元、2つなら面積、3つなら立体。y=f(x)では、x軸とf(x)との面積をx軸の特定の位置から位置まで計算する |
| 線積分 | 紐に沿って、力F(ベクトル)をかけながら進行方向にdl(微小長さと進む方向のベクトル)進むとき、F・dl(内積)を足すこと。 電磁気学では、磁界の閉曲線での線積分が線の内側の総電流と同じ(マクスウェルの第3法則の積分系)に使われる この性質を無限に長い電線に流れる電流に適用すると、電線を中心とする円周上の磁界の強さが電線からの距離に反比例することが導き出される。 |
| 面積分 | 面(布)の表面を微小正方形の面積に分け(ザルの目をイメージ)縦横を直交する微小ベクトル du dv とし、微小面積ベクトルをdS=du x dv(ベクトルの外積で面の面積を持ち面の外側に垂直なベクトル)とする。 布の表面を通り抜ける流れのベクトルV として V・dS(内積)をduとdv両方で足し算することで、面を通過する流体量や電荷量や磁界量になる。 特に、閉曲面(閉じた空間の外側壁全体)で行うことで、湧き出しがある・ないを表現できる。 電磁気学では、点電荷が周囲に作る電界がどの閉曲面でも面積分では一定になることから、点電荷を中心とする球面上の電界の強さが距離の2乗に反比例することが導き出される。 |
| 複素数表示 | 電気で交流の場合は、電流波形をsinで表すと その微分がcosになる(=sinの位相が90度ずれるのと同じ)。 マクスウェルの法則で電流・電界の微分が磁界に、磁界の微分が電界になることから、オイラーの公式で位相の変化を簡単に表現できる複素数の掛け算・割り算が使われる。 コンデンサー(コンダクタンス)やコイル(インダクタンス)が入る回路の説明が簡潔にできるため、交流で多用される。 オイラーの公式:ネイピア数 e と三角関数 sinθ・cosθ (弧度法)と複素数の間に成り立つ奇跡の美しい関係
|
複素数を物理(電磁気や電子工学)で使うことの利点
日経xtechの記事から抜粋引用紹介
https://xtech.nikkei.com/dm/article/COLUMN/20150525/419964/?P=2
交流は直流と異なり、インピーダンスという概念があります。直流の抵抗に相当するものだけでなく、抵抗と同じ単位(Ω)だけれども、周波数によって値が変化するコイルやコンデンサーのような“変な部品”が出てきます。この抵抗成分(周波数が変わってもΩの値は変わらない)とリアクタンス成分(周波数によってΩの値が変わる)をインピーダンスとして、1つの式(Z=R+jX)で表すと便利だから、複素表記を多用するのです。
オイラーの式の「eiθ」や「cosθ+i sinθ」は、単位円周上を回る振り子の位置を示したものと理解するのがコツです。この位置をxy座標で表すと、x座標はcosθ、y座標がsinθとなります(図2(a))。ただ、このようにxとyを分けて考えると、式での計算が難しくなってしまいます。
そこで、振り子の位置を「eiθ」とシンプルに示したのが、オイラーの式の指数関数表記(オイラー表記)です(図2(b))。3つの文字で重要なのはθだけです。単位円周上の振り子の位置は角度θで決まるからです。「θがeという記号の右上、iの右に乗っかっている」ことを意識するのがポイントです。
eとiについては、「単位円周上のポイントを表しているマーク」という程度に覚えていれば十分です。
――オイラー表記の利点は。
オイラー表記を用いると、直流の「オームの法則」を交流まで拡張しても計算は簡単になります。
交流では、ピーク電圧もピーク電流も先述の波動方程式で表現できます。電圧の実効値をVrms、位相をφVとすると、ピーク電圧VPは次のようになります。
VP=√2 Vrms sin(ωt-φV)
同様に、電流の実効値をIrms、位相をφIとすると、ピーク電流IPは次のようになります。
IP=√2 Irms sin(ωt-φI)
これらから、オームの法則によってインピーダンスZを計算してみます。上記のピーク電圧をピーク電流で割ります(図3)。ただし、このままだと三角関数の割り算をすることになり、計算が非常に難しい。ここでオイラー表記を使うと、計算がとても簡単になるのです。
数学では虚数表示に i を利用しますが、電磁気では 電流に i を使うので、間違えないようにするため複素数分を j で表現。
三角関数の部分は角度θで決まる振り子の位置を示したもので、eiθで表現することができます。ここでは、電圧や電流の三角関数がei(ωt-φV)やei(ωt-φI)を用いて表現できます。
このオイラー表記を使うと、インピーダンスZは図4のように計算できます。指数関数の割り算は、指数の部分を引き算すればいいですよね。三角関数の割り算に比べると非常に簡単です。
インピーダンスZは、周波数によらず一定の抵抗成分Rと、周波数によって変化するリアクタンス成分Xから成ります。Z=R+jXと表現できます。図4のインピーダンスZの計算結果を見ながら、もう一度、単位円周上の回転振り子と「eiθ(ejθ)」を思い浮かべましょう。すると、振り子の位置を横軸に投影したcos(φI-φV)に振幅を掛けたのが抵抗成分Rで、縦軸に投影したsin(φI-φV)に振幅を掛けたのがリアクタンス成分Xだと分かります。なお、計算上の円の半径はVrms/Irmsです。





