最初に、これは直流電流と静磁界の話です。それぞれが時間変化する世界ではありません。
コイルが作る磁界は、棒磁石と似ています。電流をコイルにすると、電流の周りにできる右ねじの法則の方向の回転磁界はコイルの中で集まり、できた磁界が棒磁石と同じになる。
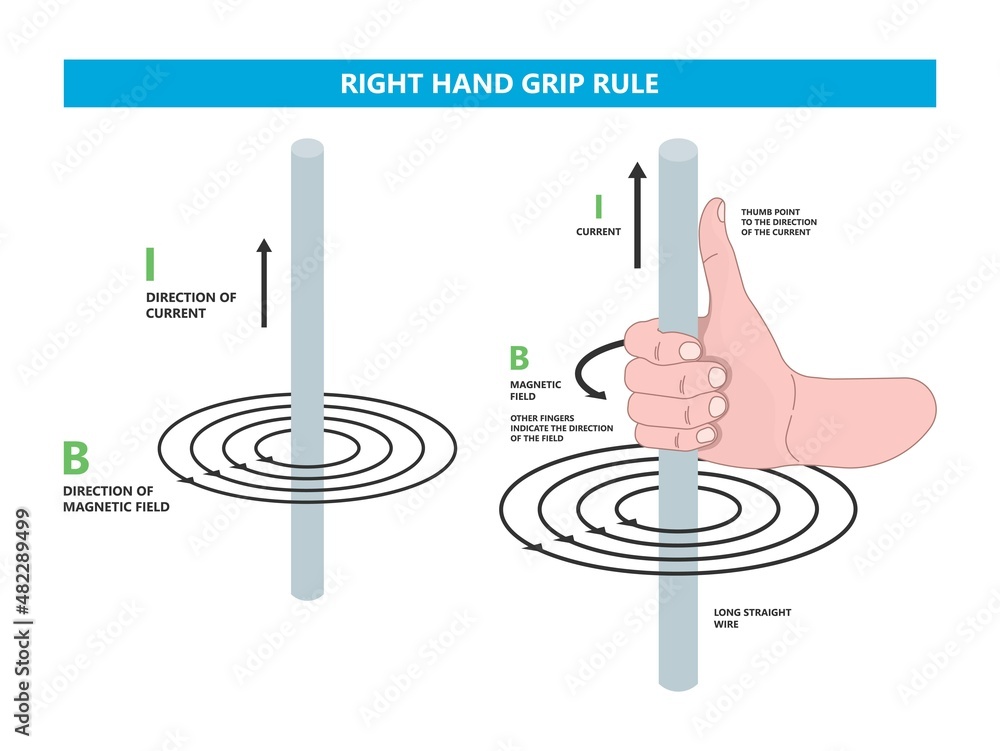
コイルに電流が流れるときにできる磁界は右手の法則。右手を握って親指以外の人差し指から小指の４本がコイルに流れる電流の向きとすると、親指がコイルの中の磁界の方向。
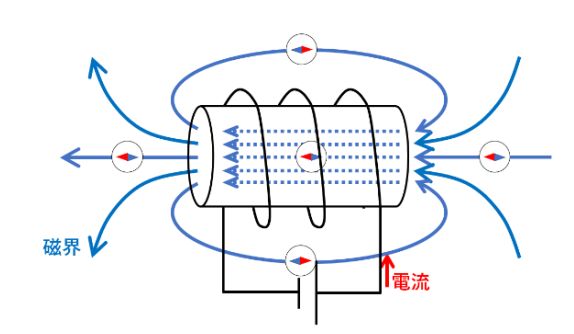
図は、東京都中央区立銀座中学校のHP掲載の https://www.chuo-tky.ed.jp/~ginza-jh/_resources/content/10001/20200428-135558.pdf から引用
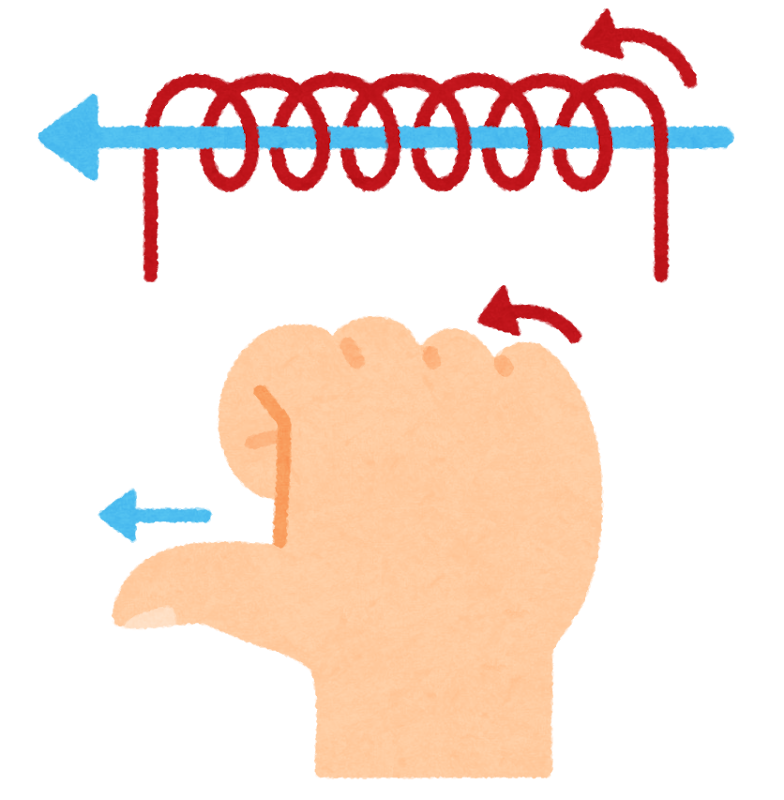
図は「いらすとや」から引用
※電流と磁界は右ねじの法則：右手を握って親指を電流の方向とすると、電流の周囲にできる磁界は握った指の方向。
このような形の円筒形のコイルをソレノイド（solenoid）と言います。その性質を考えるとき、無限に長いソレノイドを考えるとわかりやすい。
無限に長いソレノイドの磁界
無限に長いソレノイドでは、コイル中央部の磁界がビオ・サバ―ルの法則から計算により求められています。
磁束＝透磁率ｘコイル巻数ｘ電流（B＝μnI ）—- 1
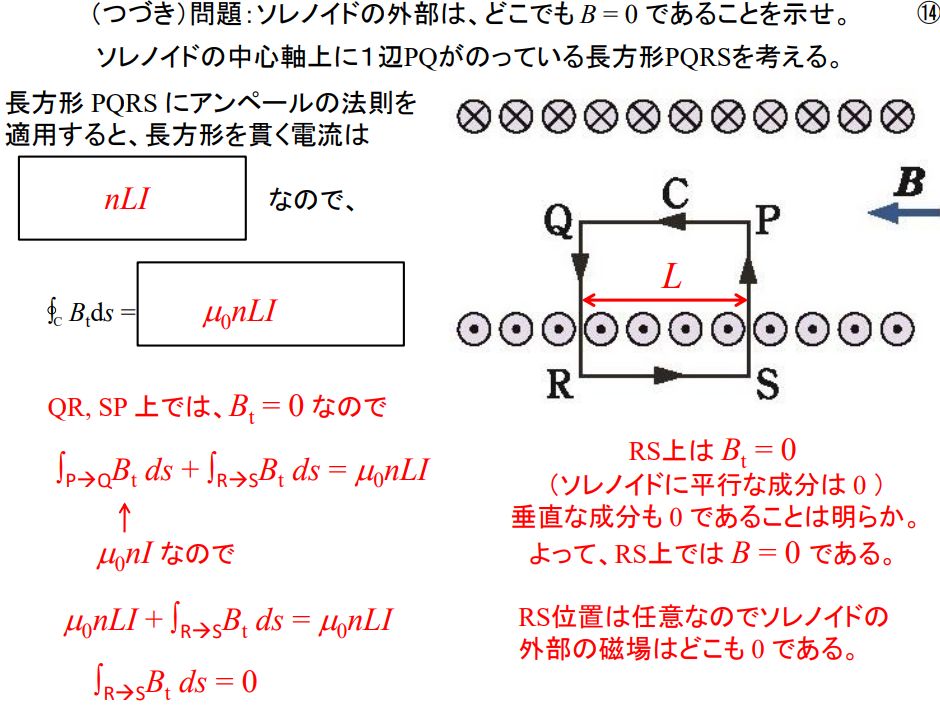
これに、電流が貫く面と面を囲む縁の磁界の関係の アンペールの法則を組み合わせる。
コイル中心線を1辺としコイル内部に任意の長方形を仮想すると（下の図でPQRS）、その長方形を貫く電流がないので発生磁界なく、一周合計した磁界＝０となり、中心部の磁束方向と同じ方向で同じ大きさの磁束が任意の場所であることになり
コイル内部は、均一にコイル中心と同じ磁束 —- 2
上記で得られた知見に、コイル中心線を1辺としコイル外部にも一辺がある長方形を仮想すると（下の図の下側のPQRS）、長方形を貫く電流でできる磁束に相当する磁束がコイル内部で発生済みのため、外部では磁束はないはずなので
コイル外部には、磁束が存在しない（磁束＝０）—- 3
次の解説図２つは、富山大学の吉田先生の物理学テキストから引用紹介
http://www3.u-toyama.ac.jp/physics/yoshida/2019/214.pdf
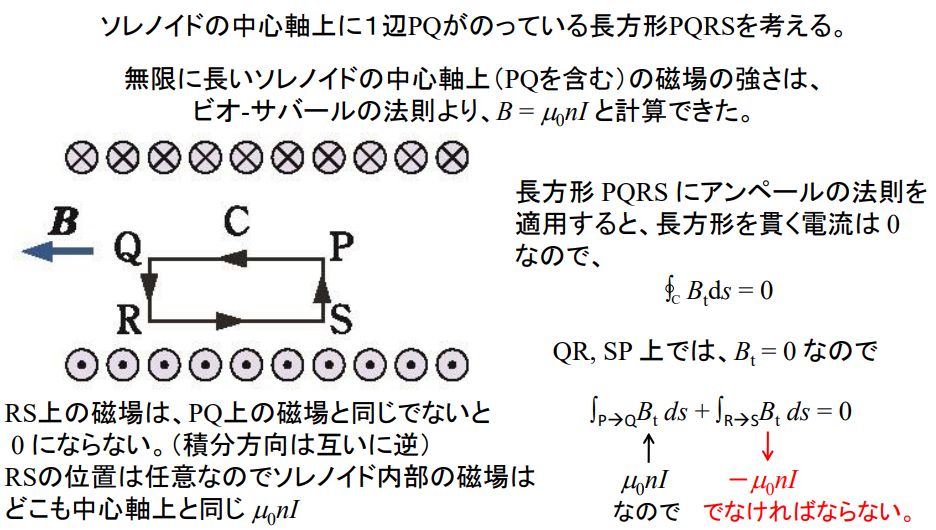
実験事実は、上記の説明を裏付けているようです。
結論１の、中心部の磁束の強さは、コイルの微小電流成分を円周方向に積分して求めているので、根拠があります。
結論の２と３は、イメージ的には、なんだか騙されているような感じもする証明ですね。
考え方の一つとしては、上の図では、上側の電線（電流）の方向＝上から下へ、 下側の電線（電流）の方向＝下から上へ、が作る磁界方向が逆なので打ち消しあう という説明の方がしっくりきますが、直径分電流からの距離が異なるので少し無理があります。
コイルから離れるとコイル径より距離の影響が大きくなり、径の差が無視できるので相殺してゼロはイメージしやすい。
※反対方向のベクトルが重なり合って相殺される例としては、コンデンサーの外側の電界が、＋の電極とーの電極の作る電界が、コンデンサーの外側で相殺しあうことで、ゼロになります。
無限長コイルでのコイル内外の磁束の考え方 その２
（私が考えた仮説です 公開資料等での証明はされていませんが だれか確かめてみていただければ）
１．上の図で、ソレノイドがコイル中心軸対称を利用、上の電線と下の電線の磁束を別々に算定し、重ね合わせる。
２．上のコイル断面（電流は紙面の上から下へ）の電流合計はnLI、 コイル中心軸を一辺とし電線断面を中心軸とする対称の長方形を仮想する。コイル軸と直角方向の磁束はないので無視。一周する磁束の線積分合計は面を貫く電流合計と一致するアンペールの法則からμnLI、上と下が大きさ同じで方向反対なので片側の辺は μnLI/2 となる。
３．同様に、下のコイル断面で、同じように仮想の長方形を仮想する。中心軸部分の辺の磁束線積分合計は、左向きで大きさは μnLI/2 （上図で長方形PQRSのPQ分に相当）
４．２と３を重ね合わせの原理で、足し合わせると 中心軸の磁束は μnLI となり公式と一致。外部では、上の電線が作る磁束と下の電線が作る磁束は大きさ同じで方向反対なので消しあってゼロ。
５．それ以後は、上記引用の富山大学の吉田先生の物理学テキストと同じで、 内部は B＝μｎLI 外部 B＝０
形状の特徴が点対称・線対称・面対称などの場合は、ビオ・サバ―ルの法則でのシミュレーションをしなくても、電磁気の基本法則を利用して簡単に磁界や電界を導くことができます。
点電荷が作る電界、面電荷が作る電界（コンデンサー）、などがその例です。
※アンペールの法則（電流が貫く面の周囲の磁束の一周合計は電流に比例）は、数学的にはベクトル場の閉曲線とその囲む面のrotの線積分と面積分のストークスの定理（「閉曲面に沿ってベクトルを線積分すると、回転(rot)を面積分したものに等しい」）と同じです。
直流電流が作る磁界は マックスウェル方程式の微分形で rot H = I が成り立ちます。 左辺の「面積分」は面を貫く電流が回りに作る磁界Hの「線積分」の合計と一致し、右辺の面を貫く電流合計と一致。
無限長コイルでのコイル内外の磁束の考え方 その３
上記の図で、アンペールの法則（電流が磁界を作る）と、回転ベクトル場の閉曲線では、ベクトルの周回線積分とベクトルのrotの面積分が一致するストークスの定理から、
１．コイル縦断面の内外を囲む、上の図ではPQRSを上下に伸ばした任意の大きな長方形を想定する。上のコイルと下のコイルは出入りの電流が相殺してゼロなので磁界の周回積分はゼロ。
→ コイル外部に磁界なし
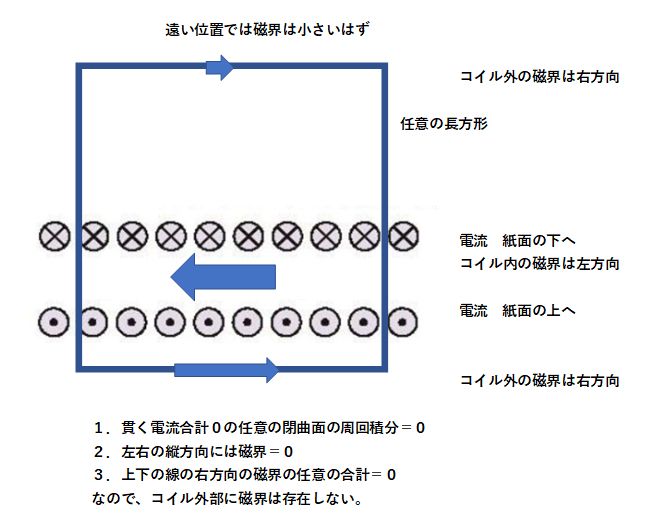
２．吉田先生の図で下側の、片側のコイルを囲むコイル内と外を１辺にする任意の長方形PQRSで、コイル外部磁界とコイル中心線に垂直方向の磁界がないから、PQ方向の線積分は長方形を貫く電流と一致。なので、コイル内部には均一な磁界 B＝μｎLI
これって、嘘みたいに簡単な説明ですね。（正しいかどうかは不明です。識者のご意見を募集）。
蛇足
この考え方を適用すると、磁界をヨークで狭い閉ループに閉じ込める場合は、その外側を囲む閉曲線では、閉曲線が囲む面の中で磁束の方向が逆となり相殺しあってゼロになるので、誘導電界も発生しない。変圧器で、ロの字型の鉄心の場合は磁界は閉じた閉ループを作ります。その外側では有害な磁界と誘導電流が発生しないのは、このためと思われます。
電気炉で、コイルの外側にヨークを設置するのもこれと同じ効果があり、電気炉設備外側には有害な磁界や誘導電流は発生しない。
しかし、個々の磁束が発生している部分を個別に囲む閉曲線では、磁束の変化は誘導電界を作り、ロの字の変圧器の鉄心に巻いたコイルには電圧が発生します。
電気炉の中の材料は、炉内耐火物を通る強い磁束の時間変化で鉄くずなど表皮部分に大きな誘導電流が流れ加熱され、隣接するコイルには誘導された逆起電力が発生し、それに抗して流す電流が投入される電力量（＝仕事）になります。
文責 藤原愼二
