2025年10月3日に北海道札幌で開催された日本鋳造協会の秋の講演大会で、鋳造工学会前会長の清水一道先生(室蘭工大・島根大学教授退官され函館高専校長就任)が講演されました。
函館高専の「校長より」

日本の産業の再生と再生に必須の鋳造を元気づけ活性化させる提言の数々と、日本の各地から若者が集まれる高専作り活動開始の紹介などを、先生製作の熱気あふれる短編プロモートビデオ含め語りました。
いつもながら清水先生が日本の素晴らしいリーダーの一人であると痛感。工学会会長と大学から転身され国立の函館高専の校長としてますます日本への貢献の意気盛ん!
講演後に清水先生と懇親する場があり、そこで奇しくも「微分と積分の話」になり、私の認識間違いを指摘いただきました。
私: 微分は細かく分けて、積分はそれを集めて再現すること。会計なら明細書が微分で、財務諸表が積分結果。
清水:積分はそれでよいけど、微分は細かく見たときの「変化率」です。
私: なるほど、変化率の意味を明確にとらえていなかった。山の斜面にいるとき、見る方向・歩く方向により標高の変化率は異なる。
その位置から、山の頂上方向を見れば変化率は+だし、険しい岩壁なら変化率はプラスで大きい。逆に下り方向を見ると変化率はーで、垂直落下しそうな崖ならマイナスが大きくなる。変化率がゼロなら水平だ。
それで電磁気のマックスウェル方程式の疑問の一部が納得できた。
右辺の時間微分は、その位置における物理量の時間経過による変化率。
左辺は右辺の変化率により発生するものが回転ベクトル場でその位置での位置変化率がROTの値になるということ。
定電流や時間で変化する電界でできる磁界は、その電流や電界の周りを回る回転ベクトル場になる。変化する磁界が作る電界もその磁界の周りを回る回転するベクトル場だ。
電界が時間のsin関数なら時間変化率が最大になるのは時刻の原点で、空間に作る回転磁界の位置変化率も最大だというのがマクスウェル方程式が意味するものだ。
電界の時間変化率が最大とはsinなら時刻の原点で、電界に直角方向に発生する磁界の位置変化率(ROT)も最大ということはsinなら位置の原点だ。
これが意味するのは、真空を電磁波が伝播するときは、電界と磁界は相互に直行し電界がsin関数の場合は同相で進行する波動になる、ということ。
電磁波
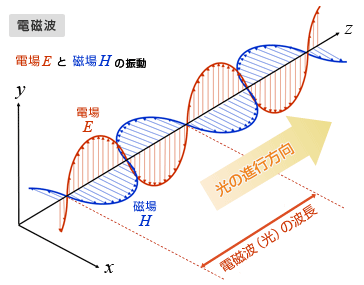
電磁波とは、空間の「電場 ( electric field ) E 」 と「磁場 ( magnetic field ) H 」が互いに振動しながら空間を伝播していく物理現象です。
3番目の式と4番目の式の対称性からも同じ変化をするものだと解る。
波の場合は、y(x,t)=f(x-ωt)+g(x+ωt) の形になってるんだと。時間の進行と位置の変化が同じ次元でつながってる。だから磁界と電界の時間変化で発生する電磁波は位置でも同相で変化する。
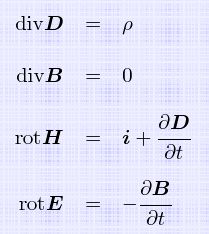
微分が、微小な部分の変化の傾向(変化率)だ、というのは重要なんですね。
蛇足: アルキメデスの原理では、水中に沈んだ物体は、その体積分の水の浮力を受ける。これは物体を細かく垂直柱に分割して、左右の水圧はバランスするけど上端と下端に働く水圧差だけ浮力が働き、その合計が浮力(船を浮かせる力)になる。これも積分になります。


